Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 32b
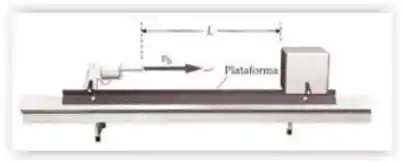
Um bloco de madeira e um revólver estão firmemente fixos nas extremidades opostas de uma longa plataforma montada sobre um trilho de ar sem atrito (figura abaixo). O bloco e o revólver estão separados de uma distância . O sistema está inicialmente em repouso. O revólver dispara uma bala que o abandona com uma velocidade , atingindo o bloco e nele se encravando. A massa da bala é e a massa do sistema revólver-plataforma-bloco é .
(b) Qual é a distância percorrida pela plataforma, enquanto a bala está em trânsito entre o revólver e o bloco?
Passo 1
(b) Olá, querido! Tudo bem?
Então, aqui a gente tem uma situação formada pelo revólver, a bala, a plataforma e o bloco. Tá todo mundo em repouso inicialmente. Por isso, a gente pode dizer que a quantidade de movimento inicial é nula
Só que a bala é disparada com velocidade . E isso gera uma velocidade no sentido oposto na plataforma. Aí o que o enunciado quer saber é o quanto essa plataforma anda entre o instante que a bala sai do revólver e o instante em que a bala atinge o bloco.
E para fazer isso a gente vai lembrar lá de cinemática. Considerado que a velocidade da plataforma é constante, a gente pode escrever que ela vai ser dada por
Onde é a velocidade da plataforma, é o tempo decorrido, ou seja, o tempo que leva para a bala sair do revólver e chegar ao bloco, e é o quanto a plataforma anda nesse tempo.
Então queremos achar :
Precisamos então da velocidade da plataforma quando a bala sai do revólver e do tempo que leva para a bala atingir o bloco. Bora descobrir!
Passo 2
O momento linear numa direção é dado por
Sendo a massa do corpo e sua velocidade.
Precisamos calcular a velocidade da plataforma logo após a bala sair do revólver. Como não há forças externas na direção do movimento, há conservação de momento linear, por isso, podemos afirmar que
Sendo que é o momento linear no instante em que a bala sai do revólver, que vai ser a soma do momento linear da bala com o momento linear da plataforma (formada pela base, o bloco e o revólver, já que todos estão fixados um ao outro). Então escrevemos:
Só que isso é igual a que por sua vez é igual a zero como vimos no primeiro passo. Então temos . Substituindo:
Isolando a velocidade da plataforma:
Passo 3
Agora a gente precisa de . Para achar esse cara, precisamos saber a velocidade da bala em relação a plataforma (velocidade relativa). Por quê?
Imagina que você está no ônibus (em movimento) e sai correndo do fundo do ônibus até a frente. Para saber o tempo que você levou você precisa usar a distância percorrida dentro do ônibus e sua velocidade relativa ao ônibus certo?
Se usar a sua velocidade em relação ao solo o resultado fica errado, porque essa velocidade é influenciada pela velocidade do ônibus.
Mesma coisa aqui! A distância está sobre a plataforma. Aí para saber o tempo que leva para a bala percorrer esse caminho, a gente precisa da velocidade da bala em relação a plataforma!
Aí precisamos montar aquela equaçãozinha de velocidade relativa:
Ou seja, a velocidade da bala em relação ao solo é igual a velocidade relativa da bala em relação a plataforma somada a velocidade da plataforma. Isolando a velocidade :
Substituindo aí a expressão que a gente achou para :
Rearrumando:
Passo 4
Aí o tempo que a bala leva para percorrer a distância vai ser dado pela equação da velocidade também:
Substituindo a expressão de :
Passo 5
Agora a gente pode calcular a distância percorrida pela plataforma.
Substituindo as expressões de e que a gente achou:
Resposta
A distância percorrida pela plataforma será: