Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 52
a)Determine uma expressao para o angulo de fase 8 para o filtro passa-baixas do Problema 51 em termos de w,ReC.（b)Determine o valor de 8no limite Oe no limitew o.Explique sua resposta.
Passo 1
Oi oi gente, como vocês estão?
Vamos fazer uma questão passo a passo?
Vamos! Vem comigo.
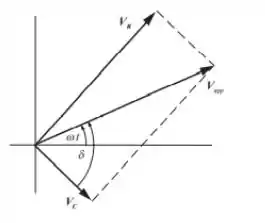
O diagrama fasorial para o filtro passa-baixa RC é mostrado à direita. são os fasores para e , respectivamente. A projeção de no eixo horizontal é e a projeção de no eixo horizontal é .
Passo 2
Letra a:
Do diagrama fasorial temos:
Use a definição de para obter:
Resolvendo para , temos:
Passo 3
Letra b:
Como . Esse comportamento faz sentido fisicamente porque, em baixas frequências, é muito grande em comparação com R e, como consequência, está em fase com .
Como . Esse comportamento faz sentido fisicamente porque, em altas frequências, é muito pequeno em comparação com R e, como consequência, está fora de fase com .
Resposta
- Como . Esse comportamento faz sentido fisicamente porque, em baixas frequências, é muito grande em comparação com R e, como consequência, está em fase com .
Como . Esse comportamento faz sentido fisicamente porque, em altas frequências, é muito pequeno em comparação com R e, como consequência, está fora de fase com .