Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 57

A expressao para o potencial eletrico dentro de uma esfea solida uniformemente carregada e dado V ( r ) = k Q 2 R 3 - r 2 R 2 onde Reo raio da esferaere a distancia ao centro.Esta expressão foi obtida no Exemplo 23-12 descobrindo,primeiramente,o campo eetrico. Neste problema , voce derivaa mesma expressao modelando aesfera como uma colecao de finas cascas esfericase,entao,somando spotenciais destas cascas em um ponto-campo dentro da esfera. O potencial dV que esta a uma distancia r do centro de uma fina casca esterica uniformemente carregada,com raio r'e uma carga por (Equacao 23-22).Considere uma esfera de raio R contendo uma carga Q que esta uniformemente distribuida e voce deseja determinar V em algum ponto dentro da esfera a)Determine uma xpressao para a carga dQ na casca esferica de raior'e espessura dr. Determine uma expressao para o potencial dV emr devido a carga uma casca de raio r'e espessura dr.(c)Integre a expressao da para determinar o otencial emr devido a todas as cargas na regiao mais afastada quer o centro da esfera.(d)Determine uma expressao para o potencial dV emr devido a carga em uma casca de raio r e espessura d,onder Sr.(e)Integre sua expressao determinar o potencial em rdevido a todas as cargas na regiao mais proxima que r ao centro da esfera.(f)Determine o potencial total V em r somando seus resultados para a Parte(c)e para a Parte(e).

Passo 1

Oi oi gente, como vocês estão?

Vamos fazer uma questão passo a passo?

Vamos! Vem comigo.

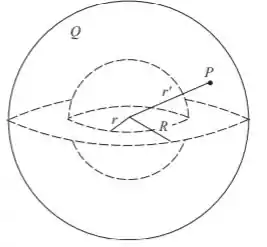
O diagrama mostra uma esfera uniformemente carregada de raio R e o ponto de campo P no qual desejamos encontrar o potencial total. Podemos usar a definição de densidade de carga para encontrar a carga dentro de uma esfera de raio r e o potencial em r devido a essa carga. Podemos expressar o potencial em r   devido à carga em uma casca de raio r ' e espessura d r ' em r ' ≥ r usando d V = k d q ' / r e então integrar esta expressão de r ' = r para r ' = R para encontrar V.

Passo 2

Letra a:

A carga d Q em uma casca de raio r ' e espessura d r ' em r ' > r é dada por:

d Q = ρ d V ' = ρ A ' d r '

Como A ' = 4 π r ' 2 : :

d Q = 4 π r ' 2 ρ d r '

Como a esfera é uniformemente carregada:

ρ = Q V = Q 4 3 π R 3 = 3 Q 4 π R 3

Substituindo ρ e simplificando, temos:

d Q = 4 π r ' 2 3 Q 4 π R 3 d r ' = 3 Q R 3 r ' 2 d r '

Passo 3

Letra b:

Expresse o potencial d V no intervalo r ≤ r ' ≤ R devido a d Q :

d V = k d Q r '

Substituindo d Q e simplificando, temos:

d V = k r ' 3 Q R 3 r ' 2 d r ' = 3 k Q R 3 r ' d r '

Passo 4

Letra c:

Integre d V de r ' = r para r ' = R para encontrar V:

V = 3 k Q R 3 ∫ r R   r ' d r ' = 3 k Q 2 R 3 R 2 - r 2

Passo 5

Letra d:

O potencial d V em r devido à carga em uma casca de raio r ' e espessura d r ' , onde r ' ≤ r , é dado por:

d V = k d Q r = k ρ d V ' r = k ρ A ' d r ' r = k ρ 4 π r ' 2 d r ' r = 4 π k ρ r r ' 2 d r '

Substituindo ρ e simplificando, temos:

d V = 4 π k r Q 4 3 π R 3 r ' 2 d r '

= 3 k Q R 3 r r ' 2 d r '

Passo 6

Letra e:

Integre de r ' = 0 a r ' = r para encontrar o potencial em r devido a toda a carga na região mais próxima do que r do centro da esfera:

V = 3 k Q R 3 r ∫ 0 r   r ' 2 d r ' = k Q R 3 r 2

Passo 7

Letra f:

A soma de nossos resultados da Parte (c) e Parte (e) é:

V = k Q R 3 r 2 + 3 k Q 2 R 3 R 2 - r 2 = k Q 2 R 3 - r 2 R 2

Resposta

  1. d Q = 4 π r ' 2 3 Q 4 π R 3 d r ' = 3 Q R 3 r ' 2 d r '
  2. d V = k r ' 3 Q R 3 r ' 2 d r ' = 3 k Q R 3 r ' d r '
  3. V = 3 k Q R 3 ∫ r R   r ' d r ' = 3 k Q 2 R 3 R 2 - r 2
  4. = 3 k Q R 3 r r ' 2 d r '
  5. V = 3 k Q R 3 r ∫ 0 r   r ' 2 d r ' = k Q R 3 r 2
  6. = k Q 2 R 3 - r 2 R 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma casca cilíndrica isolante, com raio R e comprimento L ( como o tubo de papelão de um rolo de papel higiênico), possui uma carga Q uniformemente distribuída sobre sua superfície. (a) Calcule o pote
O potencial elétrico é o mesmo em todos os pontos na superfície de um condutor. Isto significa que a densidade superficial de cargas é também a mesma em todos os pontos da superfície? Explique sua res
Uma carga de + 10,0μ C está uniformemente distribuída em uma fina casca esférica de raio 12,0c m . (Considere que o potencial seja zero bem distante das cargas). (a) Qual é magnitude do campo elétrico
Duas cascas esféricas condutoras concêntricas têm cargas iguais com sinais opostos. A casca interna tem raio externo a e carga + q ; a casca externa tem raio interno b e carga - q . Determine a difere
Determine a densidade superficial máxima de carga σ m á x á que pode existir na superfície de qualquer condutor antes que ocorra a ruptura dielétrica do ar.