Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 77
Uma amostra constituída por n moles de um gás ideal está inicialmente a uma pressão com um volume e à temperatura . O gás se expande isotermicamente até que sua pressão e
volume sejam e . Depois, ele se expande adiabaticamente até que sua temperatura seja e sua pressão e volume sejam e . A seguir, ele é comprimido isotermicamente até que sua pressão seja e seu volume , que está relacionado ao seu volume inicial por O gás é, então, comprimido adiabaticamente até voltar ao seu estado original.
- Supondo que cada processo seja quase estático, represente este ciclo em um diagrama PV. (Esse ciclo é conhecido como ciclo de Carnot para um gás ideal.)
- Mostre que o calor absorvido durante a expansão isotérmica em é
- Mostre que o calor liberado pelo gás durante a compressão isotérmica em é
- Usando o resultado que é constante para uma expansão adiabática quase estática, mostre que .
- A eficiência de um ciclo de Carnot é definida como o trabalho líquido realizado pelo gás, dividido pelo calor absorvido pelo gás. Usando a primeira lei da termodinâmica, mostre que a eficiência vale .
- Usando seus resultados das partes anteriores deste problema, mostre que
Passo 1
Legal gente, de início dá um pouco de medo essa questão, mas com calma conseguimos. A letra a é bem tranquila, já temos todos os dados que precisamos e sabemos que se trata de um ciclo de Carnot.
No diagrama PV:
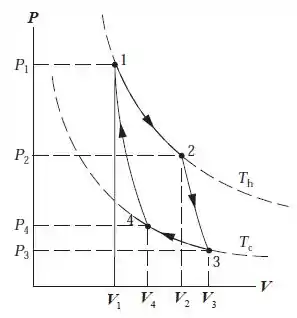
Essa foi fácil !
Na letra b queremos calcular o calor absorvido durante a expansão isotérmica. Se a temperatura é constante:
Então todo o calor absorvido pelo gás é usado para realizar trabalho e não varia sua energia interna.
O que concluímos disso? Que .
Então, pela primeira lei da termodinâmica:
Na expansão isotérmica, temos uma fórmula bem simples para o trabalho:
Se lançarmos no calor absorvido:
Bem parecida com essa letra b é a letra c. Mas agora faremos a análise para . Aqui também ocorre um processo isotérmico,
Sendo assim:
Então:
Sabendo que:
No calor:
Ou:
Onde o sinal menos indica que o calor esta sendo liberado durante o processo.
É isso ai, já fizemos três letras. Vamos continuar as demais nos próximos passos!
Passo 2
Queremos analisar a relação entre os volumes para processos adiabáticos. Neste caso, temos e ocorrendo adiabaticamente.
Assumindo que:
Podemos analisar para cada um dos intervalos. Começando por
Sabendo que a temperatura em 2 é e em 3 é
Removemos os expoentes:
Separando os volumes:
Para sabendo que a temperatura em 1 é e em 4 é
Removemos os expoentes:
Separando os volumes:
Ou seja:
Rearranjando:
Passo 3
A próxima é a letra e. E aqui queremos saber a eficiência do ciclo, sabendo que ela é dada por:
Pela primeira lei da nossa querida termodinâmica, temos:
Como estamos falando de ciclo, o estado final é igual ao inicial. E quando pensamos assim fica fácil enxergar que a temperatura também será mantida a mesma. Se não há variação da temperatura concluímos que:
Ou seja:
Agora vem algo importante. O calor do ciclo é dado pelo calor absorvido menos o liberado:
Substituindo:
Estes dois trabalhos se relacionam:
Na fórmula da eficiência:
Passo 4
Na última, mas não menos importante, letra f queremos provar que
Vamos usar para isso as equações obtidas para o calor nas letras b e c:
Da letra d obtivemos que:
Então:
Concluindo:
Resposta
Ei, a resposta está no passo a passo :)