Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 75
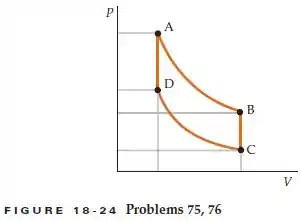
No ponto D da Figura 18-24, a pressão e a temperatura de 2 mol de um gás monoatômico ideal são 2 atm e 360 K, respectivamente. O volume do gás no ponto B do diagrama PV é igual a três vezes o volume no ponto D e sua pressão é o dobro da pressão no ponto C. Os caminhos AB e CD representam processos isotérmicos. O gás é conduzido através de um ciclo completo ao longo do caminho DABCD. Determine o trabalho realizado pelo gás e o calor por ele absorvido, em cada etapa do ciclo.
Passo 1
Bom, o exercício nos pede o trabalho total do ciclo. O trabalho total pode ser calculado como a área dessa figura geométrica, que nós não sabemos.
Então vamos com calma, para calcular o trabalho total podemos calcular o trabalho realizado por cada etapa do ciclo:
Rapidamente vocês podem perceber que o caminho de e não apresenta variação no volume.
Se não há variação no volume então não há trabalho. Não se esqueçam!
Sendo assim:
Nosso trabalho total já vai mudar de cara:
Vamos calcular cada um separadamente.
Passo 2
Começaremos calculando o trabalho do caminho Sabemos que esse processo é uma expansão isotérmica:
Neste caso o trabalho pode ser calculado como:
O problema aqui é que não sabemos nenhum dos volumes. Então vamos evidenciar o que o problema nos forneceu e ver se assim conseguimos:
Legal! Temos uma relação entre eles, certo? Então bora substituir:
Optamos por começar por esse caminho, porque tínhamos mais informações ao seu respeito. Mas bora achar o próximo.
No caminho não temos a temperatura, mas sabemos que este caminho também é isotérmico, ou seja, podemos achá-la usando o ponto A ou B, de acordo com a lei dos gases:
Não temos quase nada, para achar essas pressões e volumes. O que fazer agora?
Vamos trabalhar com o que temos. Se vocês observarem, nós temos tudo o que precisamos para calcular o volume para o ponto D usando a lei dos gases:
Vamos isolá-lo:
E agora substituir:
Temos que
E que:
Legal! Já achamos todos os volumes. Agora vamos conseguir as pressões. Neste caso podemos usar a lei dos gases para o ponto C, porque é o único ponto, além do D, para o qual temos temperatura e volume:
Isolando:
Substituindo:
Se sabemos que:
Ufa ! Fizemos muita coisa, mas agora conseguimos a temperatura do caminho usando os dados para o ponto B:
Substituindo:
Agora sim, temos tudo o que precisamos para calcular o trabalho:
Substituindo:
Para finalizar esta parte, o trabalho total, passo 1, será:
Passo 3
Não acabou ainda! Precisamos do calor de cada etapa do ciclo. Vamos por parte os caminhos que mantinham seu volume constante, usavam todo o calor absorvido para alterar sua energia interna, já que não realizavam trabalho.
Sendo assim, segundo a lei da termodinâmica:
A variação da energia pode ser calculada como:
Neste caso, g são os graus de liberdade do gás. Para um gás monoatômico, :
Para o caminho
Para o caminho
Nos demais caminhos ocorre o inverso. Sua temperatura não se altera, então o gás usa todo seu calor absorvido para realizar trabalho:
Nestes casos o trabalho pode ser definido como:
Ou seja,
Para
Para