Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 16

Esboce um diagrama ST para o ciclo Otto. (O ciclo Otto é discutido na Seção 19-1).

Passo 1

Legal galera, vamos começar relembrando o ciclo de Otto e suas etapas. Se analisarmos o que ocorre em uma máquina de Otto:

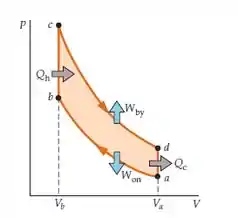
Durante a → b temos uma compressão adiabática, b → c é um aquecimento de volume constante, c → d é uma expansão adiabática e d → a é um resfriamento de volume constante.

Se precisamos de um diagrama ST, vamos analisar como o volume e a temperatura podem se relacionar com a entropia. Sabemos da relação:

∆ S = Q T

Como a → b é adiabático, d Q = 0 → d S = 0 , ou seja, a entropia é constante e a temperatura aumenta. Quando passamos de b → c o calor é inserido no sistema e ambas aumentam, entropia e temperatura. Em c → d o processo é novamente adiabático, entropia constante, enquanto a temperatura diminui. Para finalizar, de d → a o calor é removido então temos uma diminuição da entropia e da temperatura.

Passo 2

Já sabemos como as variáveis se relacionam, agora precisamos usar outros artifícios para saber como elas vão se comportar nos dois intervalos que não são adiabáticos. Precisamos lembrar que a volume constante W = 0 , então:

∆ E i n t = Q

Para um gás ideal podemos reescrever

∆ E i n t = C v ( T - T i )

Ou seja:

∆ E i n t = Q = C v ( T - T i )

Jogando na fórmula da entropia:

∆ S = C v 1 - T i T

Analisando o intervalo b → c:

∆ S = S - S b = C v 1 - T i T

No ponto final, c:

S = ∆ S + S b = C v 1 - T i T + S b

Passo 3

Bom, no passo 2 achamos uma relação entre a entropia final e inicial. Agora precisamos saber como elas se comportam no gráfico. Para idealizarmos isso podemos fazer a primeira e a segunda derivada da equação anterior, porque elas fornecem a inclinação e a concavidade do caminho.

Então vamos derivar, assumindo que se trata de um gás ideal e que C v é constante:

d S d T = C v T b T ²

d ² S d T ² = - 2 . C v T b T ³

E o que concluímos disso tudo?

Ao longo do caminho b → c, a inclinação ( d S d T ) do caminho é positiva e medida que T aumenta a inclinação diminui. Já a concavidade ( d ² S d T ² ) A concavidade do caminho é negativa para todos os valores de T.

Podemos fazer a mesma análise para d → a:

S = ∆ S + S d = C v 1 - T d T + S b

d S d T = C v T d T ²

d ² S d T ² = - 2 . C v T d T ³

E chegamos a mesma conclusão que o anterior.

Quaseee acabamos!

Passo 4

Vamos finalizar desenhando o diagrama ST.

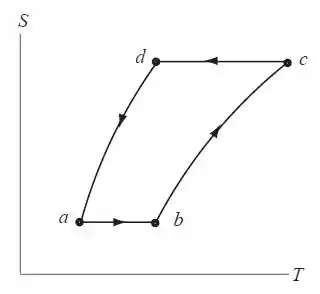
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce um diagrama SV para o ciclo Otto. (O ciclo Otto é discutido na Seção 19-1).
Os motores a diesel operam sem velas de ignição, diferentemente dos motores a gasolina. O ciclo do motor a diesel envolve a compressão adiabática do ar em um cilindro seguida da injeção de combustível
O diagrama p - V da figura mostra duas trajetórias ao longo das quais uma amostra de gás pode passar do estado a para o estado b , no qual V b = 3,0V 1 . A trajetória 1 requer que uma energia igual a
Em um motor de motocicleta, um pistão é empurrado para baixo, na direção do virabrequim, quando o combustível que está no cilindro entra em ignição, e a mistura de gases da combustão se expande adiaba
Um sistema termodinâmico vai do estado a até o estado c mostrado na Figura 19.29 pelo caminho a b c , o trabalho W realizado pelo sistema é igual a 450J . pelo caminho a d c , W é igual a 120J . As en