Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 72
Uma amostra de 1 mol de gás , a 20°C e 5 atm, expande-se adiabaticamente até que sua pressão seja igual a 1 atm. Ele é, então, aquecido à pressão constante até que sua temperatura seja novamente 20°C. Depois de atingir esta temperatura, ele é aquecido a volume constante até que sua pressão seja novamente 5 atm. A seguir, ele é comprimido à pressão constante até voltar ao seu estado original.
- Construa um diagrama PV mostrando cada processo do ciclo;
- A partir do seu gráfico, determine o trabalho realizado pelo gás durante o ciclo completo;
- Quanto calor é absorvido (ou liberado) pelo gás durante o ciclo completo?
Passo 1
Muito bem, nós precisamos construir um diagrama PV para os quatro processos descritos. Vamos analisar separadamente cada um:
1°) Expande-se adiabaticamente de 5 atm até 1 atm. Temos a pressão, mas nada sobre o volume. Então vamos começar usando a lei dos gases para achar o volume inicial:
Isolando o volume:
Transformando os dados:
Substituímos os dados:
Para um processo adiabático podemos relacionar este volume com o final:
Onde
Neste caso, g são os graus de liberdade do gás. Para um gás diatômico como o nitrogênio, :
Substituindo:
Removendo o expoente dos volumes:
Agora vamos lançar os dados:
2°) Se expande de 2 até 3 à pressão constante de 1 atm, até que sua temperatura atinja 20°C. Então no ponto final:
Isolando o volume e substituindo:
3°) Mantendo seu volume constante, , e a pressão aumenta de 1 atm até 5 atm.
4°) Ele é comprimido à pressão constante de 5 atm até voltar ao seu estado original,.
Meio chatinho né, mas conseguimos! Agora é só colocar no diagrama:
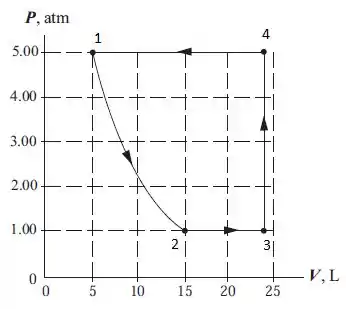
Passo 2
Na letra b precisamos calcular o trabalho pelo gráfico. Já sabemos que ele pode ser obtido calculando a área formada pela figura geométrica.
O problema aqui é que não temos muito definida esta forma, então teremos que usar aproximações. Neste caso, o desenho é formado por aproximadamente 13 quadrados, cada um com área equivalente a .
Sendo assim o trabalho será:
Transformando:
Quando analisamos o sinal, vemos que o trabalho realizado indo de 4 até 1 é negativo e maior em magnitude do que os trabalho positivos realizados de 1 até 3. Sendo assim:
Passo 3
Nos resta agora achar o calor absorvido. E para isso podemos usar a primeira lei da termodinâmica:
Quando falos de ciclo, temos os estados inicial e final iguais. Sendo assim, a temperatura inicial e final possuem o mesmo valor:
Então:
Também não temos o trabalho realizado sobre o gás, mas sabemos que existe uma relação entre eles:
Substituindo: