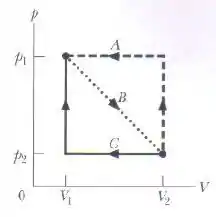
Uma amostra de gás se expande de e para e seguindo a trajetória do diagrama da figura. Em seguida, o gás é comprimido de volta para , seguindo a trajetória ou a trajetória . Calcule o trabalho líquido realizado pelo gás para o ciclo completo ao longo (a) da trajetória e (b) da trajetória .

(a) Vamos começar analisando o caminho (ou seja, pela linha pontilhada):

Na linha vertical o volume é constante, então o trabalho realizado é zero.

Na linha horizontal, temos variação de volume e a pressão é constante, então o trabalho vai ser:

A vantage de usar a integral é que você não precisa decorar qual é o sinal em cada caso. Mas pra ficar claro, quando o volume diminui, o trabalho está sendo realizado sobre o gás, e por isso o nosso (que representa o trabalho realizado pelo gás, é negativo).

Na linha diagonal é mais fácil simplesmente interpretar a integral como sendo a área abaixo do gráfico. Então vamos usar a fórmula para a área de um trapézio:

Beleza, então o trabalho nesse ciclo foi:

(a) Iradoso, agora vamos analisar caminho :

Mais uma vez, na linha vertical o volume é constante, então o trabalho realizado é zero.

Na linha horizontal, temos variação de volume e a pressão é constante, então o trabalho vai ser:

Logo:

E agora a linha diagonal é a mesma que calculamos antes, então:

E então o trabalho total aqui vai ser:

Resolvido!