Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 105
Três lentes delgadas, com a mesma distância focal de , são alinhadas ao longo de um eixo comum: a distância entre duas lentes consecutivas é . Determine a posição da imagem de um objeto pequeno colocado sobre o eixo a uma distância de à esquerda da primeira lente.
Passo 1
Vamos fazer um desenho do problema:
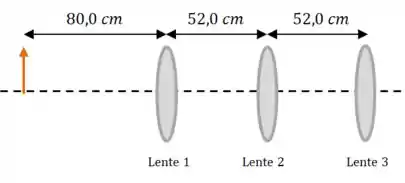
A fórmula que dá a posição da imagem formada por cada lente é:
Já que a gente só quer calcular , vamos dar uma arrumada nessa fórmula:
E invertendo os dois lados:
Beleza, e em todos os casos temos , então:
Passo 2
Ok, agora vamos aplicar isso sobre uma lente de cada vez. A distância do objeto até a primeira lente é :
Então a primeira imagem se forma à direita da primeira lente.
Isso quer dizer que a distância da primeira imagem até a segunda lente é:
Com sinal negativo porque estamos à direita da segunda lente. E então a nossa segunda imagem é formada em:
Tá, então a segunda imagem está à direita da segunda lente.
Passo 3
Olhando o desenho do primeiro passo, isso quer dizer que a distância da imagem até a terceira lente é:
E então:
Ou seja, a imagem final se forma à esquerda da terceira lente.
Em relação ao objeto, isso corresponde a essa distância aqui:
Resposta
A imagem se forma à esquerda do objeto.