Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.Problemas Adicionais - Ex. 103
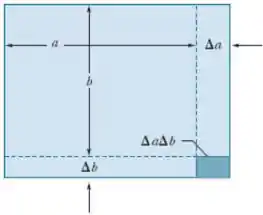
A área de uma placa retangular é e o coeficiente de dilatação linear do material da placa é . Quando a temperatura da placa sofre um aumento , o comprimento do lado aumenta e o comprimento do lado aumenta de . Determine o valor aproximado do aumento da área. (Sugestão: Despreze a parcela ).
Passo 1
Vamos encontrar uma expressão para a variação da placa em função da variação de cada lado:
E podemos desprezar , conforme a orientação do enunciado:
Passo 2
Agora vamos escrever expressões para as dilatações de cada um dos lados da placa:
E substituindo isso na equação anterior:
E agora é só substituir os valores numéricos:
Resposta
A variação da área é .
Exercícios de Livros Relacionados
Um tanque de aço é completamente cheio com 1,90 m3 de etanol quando tanto o tanque quanto o etanol estão à temperatura de 32,0 ºC. Quando o tanque e seu conteúdo tiverem esfriado até 18,0 ºC, que volu
Um frasco de vidro com volume igual a 1.000,00 cm³ a 0,0 ºC está completamente cheio de mercúrio a essa mesma temperatura. Quando esse sistema é aquecido até 55,0 ºC, um volume de 8,95 cm3 de mercúrio
Você é o novo engenheiro mecânico da Motores Inc. e foi incumbido de projetar pistões de latão para deslizarem dentro de cilindros de aço. Os motores em que esses pistões serão usados funcionarão entr
Um torneiro mecânico faz um furo de diâmetro igual a 1,35 cm em uma placa de aço a uma temperatura de 25,0 ºC. Qual é a área da seção reta do orifício (a) a 25,0 ºC; (b) quando a temperatura da placa
O diâmetro da moeda de um centavo de dólar americano é 1,9000 cm a 20,0 ºC. A moeda é feita com uma liga metálica ( quase toda de zinco), cujo coeficiente de dilatação linear é igual a 2,6 x 10- 5K-1