Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.Problemas Adicionais - Ex. 98
Para reduzir o congestionamento das estradas entre duas cidades como Boston e Washington, os engenherios propuseram a construção de um túnel de estrada de ferro ligando diretamente as duas cidades. Um trem sem motor partindo do repouso, desceria durante a primeira parte da viagem e subiria durante a segunda parte, até chegar ao destino. Supondo que a Terra é uma esfera homogênea e ignornado as forças de atrito, calcule o tempo de duração da viagem.
Passo 1
A grande dificuldade nessa questão é o fato de que a força gravitacional varia conforme a distância do trem até o centro da Terra também varia.
Precisamos achar uma expressão que dê o módulo dessa força para cada posição do trem no interior da Terra.
Pelo teorema das cascas esféricas, sabemos que a gravidade no interior da Terra é dada por:
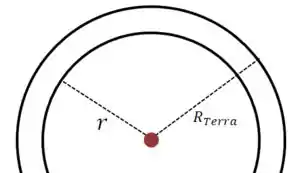
Passo 2
Mas a força que impulsiona o trem ao longo do túnel não é exatamente , mas sim a sua projeção na direção do túnel:
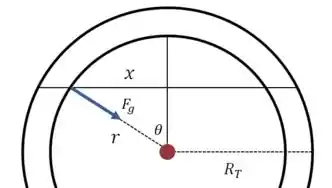
E, pelo desenho, podemos reescrever o seno através dos valores de (distância percorrida ao longo do túnel) e :
Então, pela segunda lei de Newton:
Agora podemos dividir tudo por :
Passo 3
Essa é a famosa equação do oscilador harmônico. Nesse caso, nós sabemos que o termo que multiplica é o quadrado da frequência angular do movimento:
Agora vamos reescrever em função do período que queremos calcular:
Agora vamos substituir os valores numéricos:
Mas é o período de uma oscilação completa (ida e volta), e só queremos a duração do trajeto entre as duas cidades, ou seja:
Resposta
O tempo de duração da viagem é minutos.