Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 8
Os astronautas na estação Espacial Internacional, aparentemente sem peso, monitoram cuidadosamente sua massa, porque sabe-se que uma perda significante de massa corportal pode caisar sérios problemas médicos. Dê um exemplo de um equipamento que você projetaria para medir a massa de um atronauta em órbita na estação espacial.
Passo 1
E aí galera, tudo certo? Imagina aí... lá na estação espacial não tem gravidade , então não dá para usar uma balança para medir a massa dos astronautas. Por que?
Porque a balança que a gente usa aqui mede a força que é aplicada nela quando a gente sobe na balança. Essa força medida é a força peso .
A força peso é dada pelo produto entre massa e a gravidade:
Conseguimos achar a massa por ela fazendo:
Então o que a balança faz é medir , mas nos dá o valor de porque ela já sabe o valor de .
Mas se não há gravidade , como na estação, não há força peso . Assim não há nada que a balança possa medir.
E aí que entra a pergunta: como vamos achar então?
Passo 2
A gente pode pensar em outra equação que a gente viu e usa a massa, a equação da segunda lei de Newton:
Onde é a força resultante sobre o astronauta, é a massa dele e é sua aceleração.
Isolando que a gente quer:
Então a gente precisa de um equipamento que nos dê a força resultante sobre o astronauta e sua aceleração, ok? Com essas duas informações, a gente descobre .
Passo 3
Como sobre o astronauta não tem nenhuma força, já que ele está no espaço. Se a gente imprimir uma força sobre o astronauta, essa vai ser a força resultante sobre ele!
Então, não precisaríamos medir a força, só saber a força que nosso equipamento usou. Um objeto que pode imprimir uma força conhecida é uma mola de rigidez conhecida . Porque aí a gente consegue medir sua força pela equaçãozinha:
Logo, uma solução para o nosso equipamento seria uma mola esticada que puxa o astronauta depois que liberada. Mas inicialmente ela tem uma deformação conhecida e sabemoso seu . Assim a gente descobre que é a força que a mola faz no astronauta.
Que por sua vez é a força resultante sobre o astronauta.
Como precisamos da aceleração, é só medir a aceleração que o astronauta ganha nesse movimento de ser puxado. Isso pode ser medido através de sistemas que usam uma câmera ou sensor e que conseguem medir a as propriedades do movimento dele, inclusive sua aceleração.
Fica algo assim:
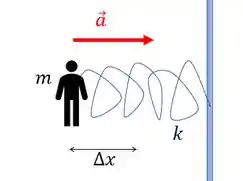
Com esses dados, usamos a segunda lei de Newton para descobrir .
Resposta
Discussão nos passos