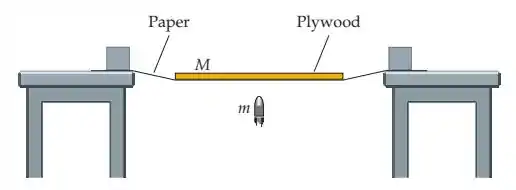
Uma bala de massa é disparada verticalmente de baixo, contra uma fina chapa horizontal de compensado, de massa , que está inicialmente em repouso, apoiada sobre uma fina folha de papel. A bala atravessa o compensado, que se eleva até uma altura acima da folha de papel antes de cair. A bala continua subindo até uma altura acima do papel. (a) Expresse, em termos de e de , as velocidades para cima da bala e do compensado, imediatamente após a bala ter atravessado o compensado. (b) Qual é a rapidez inicial da bala? (c) Qual é a energia mecânica do sistema antes e após a colisão inelástica? (d) Quanta energia mecânica é dissipada durante a colisão?
Passo 1
a) Oi, querido! Tudo bem?
Vamos olhar para a bala primeiro. Logo após atravessar o compensado, a bala tem uma velocidade . E depois ela sobe livremente até atingir uma velocidade máxima , em relação ao ponto em que ela estava ao atravessar o compensado.
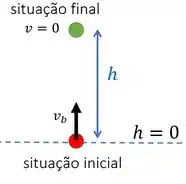
Aí ele quer . Percebe que ele dá uma altura máxima em um ponto e quer a velocidade em outro ponto, onde . Isso é uma dica para gente usar a conservação de energia!
Temos
A energia inicial vai ser só cinética porque de acordo com nosso referencial. E a energia final vai ser só potencial gravitacional porque na altura máxima a velocidade é nula, e assim também a energia cinética ().
Substituindo a expressão de cada uma dessas energias:
Isolando quem a gente quer:
Passo 2
Para o compensado, temos uma situação bem similar. Ele dá a altura máxima dele , e quer a velocidade dele logo após ser atravessado pela bala.
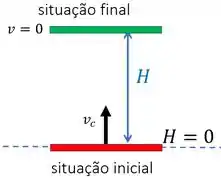
Vamos fazer o mesmo que fizemos no passo anterior e usar a conservação de energia:
A energia inicial vai ser só cinética porque de acordo com nosso referencial. E a energia final vai ser só potencial gravitacional porque na altura máxima a velocidade é nula, e assim também a energia cinética ().
Substituindo a expressão de cada uma dessas energias e isolando quem a gente quer:
Passo 3
b) Cara, a gente tem a velocidade da bala depois da colisão e quer saber a velocidade dela antes da colisão . O que a gente vai usar? Cara, pensou em colisão, pensa em conservação da quantidade do movimento:
Inicialmente, só a bala está em momento, então a quantidade de movimento é dada somente pela bala, e vale
Já logo depois da colisão, os dois objetos se movem, então a quantidade de movimento é a soma das quantidades de cada um:
Onde e são as velocidades que a gente achou no item anterior. E é a massa da bala e a massa do compensado. Substituindo tudo na conservação:
Dividindo tudo por :
Substituindo as expressões de e que a gente tem:
Passo 4
c) Cara, ele quer saber a energia mecânica antes e depois da colisão. Como é imediatamente antes da colisão e logo depois da colisão, podemos considerar que não há diferença de altura entre esses dois momentos. Então vamos desprezar a energia potencial gravitacional.
Assim, inicialmente, a energia era apenas a energia cinética da bala, porque ela era a única em movimento:
Substituindo a expressão da velocidade:
Colocando em evidência:
Passo 5
Depois da colisão, vamos ter energia cinética da bala e do compensado. Então a gente soma essas duas bonitas:
Substituindo as expressões de cada uma das velocidades:
Colocando em evidência:
Passo 6
d) Cara, a energia dissipada é a variação de energia mecânica que o sistema sofreu ao comparar o antes e depois da colisão.
Então o que a gente precisa fazer é calcular essa variação a partir das energias que a gente achou a partir do item anterior:
Substituindo as expressões que a gente achou:
Resposta
a)
b)
c)
d)