Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 42
Use o teorema dos eixos paralelos e o resultado do problema 41 para encontrar o momento de inércia do sistema de quatro partículas da figura 9-45 em relação a um eixo que passa pelo centro de massa e que é paralelo ao eixo . Confira seu resultado fazendo o cálculo diretamente.
Passo 1
Olá, querido! Tudo bem?
Ele fala para usar o resultado do exercício anterior para achar o momento de inércia desse sistema de partículas da figura em relação a um eixo que passa pelo centro de massa desse sistema e é paralelo a . Então é uma boa a gente dar uma olhada nos dados do exercício 41.
A gente tinha lá esse sistema de partículas, onde e .
E o nosso resultado do exercício 41 (o nosso resultado para esse exercício está diferente do gabarito do livro, tá? Mas a gente está certinho) diz que o momento de inércia do sistema em relação ao eixo é
E ele pede para usar o teorema dos eixo paralelos para achar a partir desses valores. E o que esse teorema diz? Pelo teorema dos eixos paralelos,
Onde é o momento de inércia de um sistema com relação a um eixo que atravessa seu centro de massa, é a massa do sistema e a distância entre os eixos.
Vamos usar essas informações para achar o desse sistema aí. Bora!
Passo 2
Então, percebe que do teorema é o momento de inércia em relação a um eixo paralelo ao eixo que passa pelo CM. No nosso caso, esse eixo pode ser o Então fazemos . Aí o teorema fica
Isolando quem a gente quer achar
Sabemos que :
Então para achar a gente precisa desse termo .
Passo 3
é a massa do sistema, então vamos somar todas as massas das partículas para achar ele:
E quem é ? Ele é a distância entre o eixo e o CM. Mas onde está o centro de massa desse sistema?
Vamos olhar nosso sistema, lembrando que e . Daí você pode perceber que temos dois eixos de simetria na distribuição das massas dessas partículas:
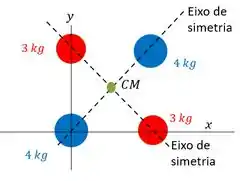
E aí, quando a gente tem dois eixos de simetria, o centro de massa está na interseção desses dois caras. Logo nosso CM é essa bolinha verde.
Então, a distância entre o CM e o eixo (que está na interseção entre e ), vai ser a metade da diagonal do quadrado de lado . Para achar a diagonal de uma quadrado, a gente multiplica o lado por . Então a diagonal vale e temos que:
Passo 4
Daí é substituir os valores que a gente achou no teorema
Passo 5
Agora vamos confirmar esse resultado calculando o momento de inércia desse sistema diretamente. A gente vai calcular o momento de inércia de cada massa em relação ao eixo que passa pelo CM e somar.
O momento de inércia de uma partícula é
Sendo que é a massa de uma partícula e é a distância dela ao CM. Percebe que todas as nossas partículas distam do CM, que é a metade da diagonal do quadrado. Então vamos ter
Aí calculando o momento de inércia de cada partícula e somando, vamos ter:
Percebe que deu igualzinho ao nosso valor achado pelo teorema dos eixos paralelos 😊