Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 29.Exercícios - Ex. 56
Uma barra com comprimento está livre para deslizar sem atrito sobre trilhos horizontais, como indica a Figura P29.56. Há um campo magnético uniforme , orientado para dentro do plano da figura. Em uma das extremidades dos trilhos há uma bateria com fem e uma chave S. A barra possui massa de e resistência de , e todas as demais resistências no circuito podem ser ignoradas. A chave é fechada no instante .
(a) Faça um desenho da velocidade escalar da barra em função do tempo.
(b) Logo após a chave ser fechada, qual é a aceleração da barra?
(c) Qual é a aceleração da barra quando sua velocidade escalar é igual a ?
(d) Qual é a velocidade terminal da barra?
Passo 1
Olá, tudo bem? Vou ajudar você aqui!
Letra (a):
Da segunda lei de Newton temos:
E a corrente se relaciona com a velocidade, então temos:
E integrando dos dois lados temos:
É uma curva exponencial e o gráfico fica mais ou menos assim:
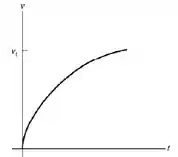
Passo 2
Letra (b):
Logo após a chave ser fechada, temos que e , sendo assim a força é:
E a aceleração é dada pela segunda lei:
Passo 3
Letra (c):
Quando a velocidade é a aceleração pode ser calculada da expressão do passo um:
Passo 4
Letra (d):
A velocidade terminal é quando o termo da exponencial vai a zero, o seja :
Resposta
