Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 29.Exercícios - Ex. 26
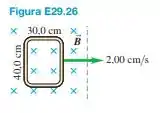
Um retângulo que mede 30,0 cm por 40,0 cm está localizado no interior de um campo magnético espacialmente uniforme de 1,25 T, com o campo perpendicular ao plano da bobina (Figura E29.26). A bobina é retirada a uma taxa regular de 2,00 cm/s, movendo-se perpendicularmente às linhas de campo. A região do campo termina bruscamente, conforme indicado. Determine a fem induzida nessa bobina, quando ela está: (a) inteiramente no interior do campo; (b) parcialmente no interior do campo; (c) totalmente fora do campo.
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
Vamos identificar , uma bobina retangular é alinhada perpendicularmente às linhas do campo magnético e puxando para fora a uma taxa constante. Neste caso, o fluxo magnético ligado através da bobina muda gradualmente. De acordo com a lei de indução eletromagnética de Faraday, a mudança no fluxo magnético induz uma fem através da bobina.
Configurando, temos que o fluxo magnético ligado através da bobina é dado pela relação
Onde , o número de voltas da bobina é , a área da bobina é , a magnitude do campo magnético é e o ângulo entre as linhas do campo magnético para o vetor normal da superfície da bobina é .
Usando a lei de indução eletromagnética de Faraday, a fem induzida através da bobina é
Passo 2
- No caso da bobina estar toda dentro do campo magnético uniforme, a força do campo magnético que atua na bobina permanece inalterada nesta região. Assim, o fluxo magnético ligado através da bobina também é constante nesta região do campo magnético uniforme.
- No caso da bobina estar parcialmente dentro do campo magnético, o campo magnético ligado através da área da bobina está mudando. Se deixarmos ser o comprimento parcial da bobina dentro do campo, então a área da bobina associada ao campo é .
- No caso da bobina esta totalmente fora do campo magnético uniforme, a intensidade do campo magnético atuando na bobina permanece inalterada nesta região. Portanto, o fluxo magnético ligado através da bobina também é constante nesta região do campo magnético uniforme.
Como .
O valor de
Consequentemente , a taxa zero de mudança do fluxo magnético não pode induzir um fem através da bobina. Assim, quando a bobina está toda dentro do campo magnético uniforme, a fem induzida através da bobina para esta região é momentânea .
Passo 3
Onde a largura da bobina retangular e dada como 40 cm.
Passo 4
Para uma bobina de uma volta
Magnitude do campo magnético,
A bobina está puxando a uma taxa constante, .
Como o plano perpendicular da bobina está puxando o campo magnético, o ângulo entre as linhas do campo magnético para o vetor normal da superfície da bobina é
Portanto, o fluxo magnético ligado através da bobina é
Passo 5
Usando a lei de indução eletromagnética de Faraday, a fem induzida através da bobina é calculada como :
Onde o termo corresponde à velocidade de tração da bobina.
Logo, ao substituirmos o temos por , teremos
Substituindo os valores numéricos dados na equação acima,
Portanto, a magnitude da fem induzida na bobina desta região é de
Passo 6
Como
O valor de
Passo 3
Consequentemente, a taxa zero de mudança do fluxo magnético não pode induzir um fem através da bobina. Sendo assim, quando a bobina está fora do campo magnético uniforme, a fem induzida através da bobina para esta região é momentânea