Enunciado

Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 29.Exercícios - Ex. 34

O sangue contém íons positivos e negativos e, sendo assim, é um condutor. Um vaso

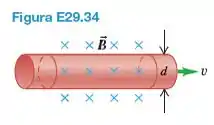
sanguíneo, portanto, pode ser visto como um fio elétrico. Podemos até mesmo imaginar o sangue fluindo como uma série de caminhos condutores paralelos, cuja espessura tem o diâmetro d do vaso, movendo-se com velocidade v. (Ver Figura E29.34.)

(a) Se o vaso sanguíneo for colocado em um campo magnético perpendicular ao vaso, como na figura, mostre que a diferença de potencial de movimento induzida por ele é .

(b) Se você espera que o sangue esteja fluindo a para um vaso de de diâmetro, que intensidade de campo magnético será necessária para produzir uma diferença de potencial de ?

(c) Mostre que a taxa de volume do fluxo (R) do sangue é igual a . (Nota: embora o método desenvolvido aqui seja útil na medição da taxa de fluxo sanguíneo em um vaso, ele é limitado ao uso na cirurgia, pois a medição do potencial precisa ser feita diretamente através do vaso.)

Passo 1

Olá, tudo bem? Vou ajudar você aqui!

Letra (a):

Considerando o vaso como um condutor imerso em um campo magnético, temos um deslocamento de cargas por causa da força magnética, certo? Isso gera um acúmulo de cargas nas extremidades desse vaso e que por sua vez gera um campo elétrico associado. Nas partículas então agem duas forças: elétrica e a magnética, e elas estão em equilíbrio:

O módulo da diferença de potencial nas extremidades do vaso é igual ao produto do campo pelo diâmetro do vaso:

Passo 2

Letra (b):

Pela expressão do passo anterior temos:

Passo 3

Letra (c):

A vazão é:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espira quadrada é mantida em um campo magnético uniforme de 0,24 T perpendicular ao plano da espira. O comprimento dos lados do quadrado está diminuindo a uma taxa constante de 5,0 cm/s. Qual é a

Uma espira retangular de lados a e b afasta-se com velocidade v = vx ^ de um fio retilíneo muito longo, que transporta corrente contínua de intensidade I . A espira tem resistência R e autoindutância

Uma espira retangular de lados a e b de resistência R cai num plano vertical e atravessa uma camada onde existe um campo B uniforme horizontal (fig.).Repita o cálculo num instante posterior, em que a

Uma espira circular de raio a tem no seu centro uma outra espira de raio b ≪ a . Os planos das duas espiras formam entre si um ângulo θ . Calcule a indutância mútua entre elas.