Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 9.Problemas - Ex. 4bcd
Uma barra horizontal de comprimento e massa escorrega com atrito desprezível sobre dois trilhos verticais unidos por uma haste horizontal fixa de resistência . A resistência da barra e dos trilhos pode ser desprezada em confronto com . O conjunto está situado num campo magnético horizontal uniforme, orientado para dentro do campo da figura.
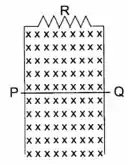
- Qual é a aceleração da barra?
- Com que velocidade terminal ela cai?
- Qual é o valor correspondente da corrente?
Passo 1
Para o item (b) usaremos as a segunda lei de Newton. Para isto, precisamos lembrar que a força peso é
E que a força magnética é dada por
Como não sabemos quem é a corrente elétrica, podemos identificá-la pelo fluxo do campo magnético. Para isto, teremos que levar em consideração que a área varia quando com a distância
Lembrando da relação
Passo 2
Agora, podemos escrever, pela segunda lei de Newton, que
Passo 3
Agora vamos para o item (c).
Como já conhecemos a aceleração, podemos lembrar que
Vamos fazer uns ajustes para diminuir a probabilidade de erros! Vamos chamar
Agora podemos escrever que
Passo 4
Solucionando a equação diferencial teremos uma solução do tipo
Aplicando as condições iniciais obtemos
Passo 5
Agora, no item (d) só precisamos substituir o novo na expressão da corrente que escrevemos anteriormente