Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 41
Uma barra não condutora carregada, com um comprimento de e uma seção reta de , está no semieixo positivo com uma das extremidades na origem. A densidade volumétrica de carga é a carga por unidade de volume em coulombs por metro cúbico. Determine quantos elétrons em excesso existem na barra (a) se pé uniforme, com um valor de ; (b) se o valor de pé dado pela equação , em que
Passo 1
- Nessa questão, nos é apresentada a situação do desenho: uma barra sobre o eixo com uma certa densidade de carga. Primeiro, como gazer para calcular a carga que essa barra possui se a sua densidade é constante? Vou te mostrar!
- Na letra b) a história é um pouco diferente por que a densidade varia com o comprimento da barra: ela não é uniforme nesse caso. Mas não se desespere, por que a resolução não muda muito nesse caso. Nós só precisamos calcular uma integral um pouco diferente, sendo :
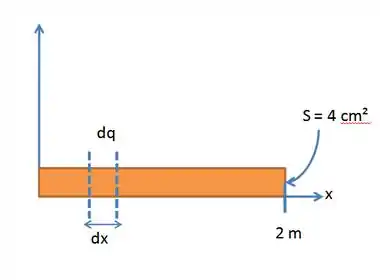
De modo geral, imagina que essa barra é formada pela soma de infinitas pequenas barras de carga , como mostrado na figura. Essas carguinhassão iguais ao produto da densidade de carga pelo pequenino volume delas. Esse volume é o produto da área transversal pelo comprimento delas. Daí, temos:
Nesse caso:
Passo 2
Beleza! Agora a gente usa o recurso da integral para encontrarmos essa carga:
Mas a questão pede pra gente outra coisa: o excesso de elétrons nessa barra. Para isso, só precisamos então dividir o valor dessa carga pela carga de um elétron para descobrirmos a quantos elétrons equivale essa carga total negativa:
elétrons
Passo 3
Fazendo assim, temos:
Passo 2
Beleza! Daí, agora é só substituirmos os valores nessa expressão e calcularmos o excesso de elétrons como na letra a) :
elétrons