Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 79
A barra do problema 34.78 é encurtada e a distância entre seus vértices passa para ; os raios de curvatura das extremidades permanecem inalterados. Como no problema 34.78, o objeto para a superfície da extremidade esquerda é uma seta situada à esquerda do vértices dessa superfície. A seta possui altura de e está localizada perpendicularmente ao eixo da barra. (a) Qual é a distância do objeto para a superfície da extremidade direita da barra? (b) O objeto para essa superfície é real ou virtual? (c) Qual é a posição da imagem final? (d) A imagem final é real ou virtual? Ela é direita ou inertida em relação ao objeto original? (e) Qual é a altura da imagem final?
Passo 1
(a) O primeiro passo é fazer um desenho da situação:
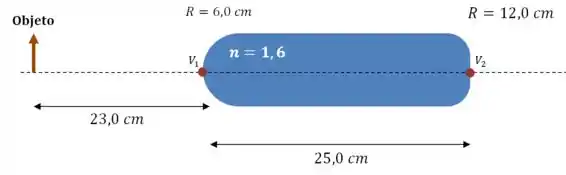
Do ponto de vista da superfície direita, o objeto é, na verdade, a imagem formada pela superfície esquerda.
Vamos calcular a posição dessa imagem (que vamos chamar de Imagem 1):
E todos esses valores estão ali no desenho, menos o , que queremos calcular:
Então a Imagem 1 está a do ponto . Por isso, a distância até a superfície da direita (o ponto ) é:
Ou seja, o “objeto” (que é a Imagem 1) está à direita da superfície da direita.
(b) Nesse caso, já que o objeto está do lado de fora da barra, do mesmo lado da luz que sai da superfície, então ele é virtual.
Passo 2
(c) Pra calcular a posição da imagem final, a gente precisa ver o que acontece quando a Imagem 1 incide sobre a superfície da direita.
Vamos usar a mesma fórmula de antes:
Pelo que fizemos no passo de cima, :
Então a imagem final fica à direita da superfície direita.
Passo 3
(d) Já que a posição da imagem é positiva, então a imagem é real.
Pra dizer se ela é invertida ou direita, temos que calcular a amplificação em cada um dos dois processos que a gente viu.
No primeiro, em que Imagem 1 é formada:
E no segundo, em que a imagem final é formada:
Então a magnificação total é:
Como a amplificação total é negativa, a imagem final é invertida em relação ao objeto original.
Passo 4
(e) Pra calcular a altura da imagem final, vamos usar essa fórmula aqui:
Como a altura do objeto original é , a altura da imagem final é:
O sinal negativo só diz que a imagem é invertida.
Resposta
(a) O objeto está à direita da superfície.
(b) Para essa superfície, o objeto é virtual.
(c) A imagem final está à direita da superfície direita.
(d) A imagem final é real e invertida.
(e) A imagem final tem de altura.