Duas lentes delgadas com distâncias focais de módulo , a rimeira divergente e a segunda convergente, são colocadas a de distância uma da outra. Um objeto com de altura é colocado à esquerda da primeira lente (divergente). (a) Qual é a posição da imagem formada pela primeira lente? (b) A que distância do objeto é formada a imagem final? (c) A imagem final é real ou virtual? (d) Qual é a altura da imagem final? A imagem final é direita ou invertida?

(b) Beleza, essa imagem vai servir de objeto para a lente convergente!

A imagem está à esquerda da primeira lente, que está à esquerda da segunda lente:

Agora é só fazer a mesma conta de antes, mas agora, como a lente é convergente, o foco vai ter sinal positivo:

Essa é a distância da imagem final até a lente convergente. Mas o que o enunciado pediu foi a distância da imagem final até o objeto.

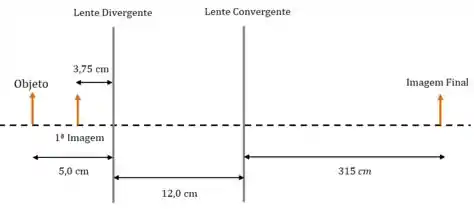
O desenho tá totalmente fora de escala, mas já ajuda a calcular essa distância:

(c) A imagem final aparece do outro lado da lente convergente, como no nosso desenho do passo anterior.

Além disso, encontramos , isso quer dizer que a imagem é real.

(d) Pra encontrar a altura da imagem final a gente precisa calcular a ampliação de cada uma das lentes.

A fórmula é essa aqui:

Então é só voltar nos passos de cima pra ver os valores que nós usamos em e .

No caso da primeira lente:

E no caso da segunda:

Então a ampliação total é a seguinte:

E a altura da imagem vai obedecer essa fórmula aqui:

O sinal negativo diz que a imagem é invertida.