Um bastão condutor de comprimento gira a uma rapidez angular constante em torno de uma de suas extremidades, em um plano perpendicular a um campo magnético uniforme . (a) Mostre que a diferença de potencial entre as extremidades do bastão é . (b) Seja o ângulo entre o bastão girando e linha tracejada definida por . Mostre que a área da região, no formato de torna percorrida pelo bastão durante o tempo é . (c) Calcule o fluxo através desta área e aplique (Lei de Faraday) para mostrar que a fem induzida por movimento é dada por .
Passo 1
Fala galera, tudo beleza?
- Então, podemos imaginar a barra formada por uma série de “pequenas barras”, cada uma velocidade , de modo que cada uma dessas barrinhas tem uma fem do movimento dada por
- Aqui, bastará aplicar uma regra de três simples. Sabemos que quando o ângulo percorrido por uma circunferência é , então sua área é . Logo, quando o ângulo for sua área será :
- Aplicando a Lei de Faraday,
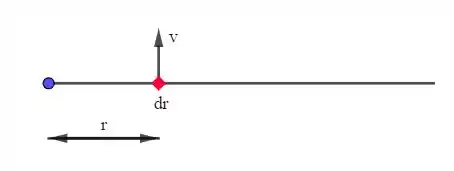
Dessa maneira, a fem total será a soma da fem de cada uma dessas barrinhas, ou seja,
Passo 2
Logo,
Para a gente, o raio da circunferência é o próprio comprimento da barra. Assim,
O fluxo será
Assim,
conforme queríamos mostrar!
Resposta
Ei, a resposta está no passo a passo :)