Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 17
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor indicado na Figura , quando
a chave é aberta depois de ficar fechada durante alguns minutos;
quando a bobina se aproxima da bobina enquanto a chave permanece fechada;
quando o valor da resistência diminui enquanto a chave permanece fechada.
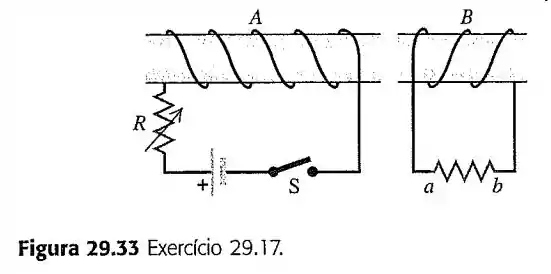
Passo 1
Quando a chave está fechada o campo magnético na bobina segue o sentido da corrente e vai da esquerda para a direita (pois pela regra da mão direita temos que pegar a corrente que entra no tubo). Tal como nos mostra a figura.
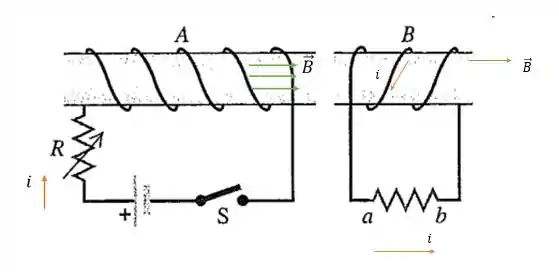
Quando cessa esse campo magnético a bobina da direita sente falta desse campo magnético que tinha antes e passa a produzir um campo magnético para a direita também e para isso a corrente induzida passa a ter o sentido horário. Ou de para no resistor. (a diferença de sentido é por conta da mudança de sentido da enrolação da espira , a espira é enrolada inclinada para baixo e a espira para cima, dando pela regra da mão direita uma mudança de sentido do campo magnético).
Passo 2
Pegando o centro do eixo da bobina em nós temos uma queda na intensidade a medida que a bobina se afasta da bobina .
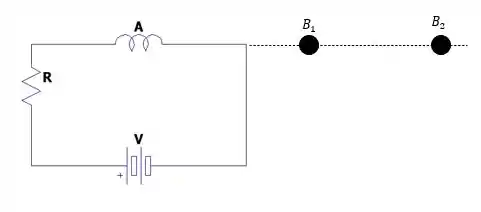
Ou seja o campo em é maior que em . Então quando a bobina se aproxima de pela Lei de Lenz acaba por surgir um campo magnético para a esquerda de forma a repelir o campo magnético extra que aponta para a direita advinda da bobina em . E como esse campo magnético induzido aponta para a esquerda então corre na bobina uma corrente induzida no sentido anti-horário. Ou de para no resistor.
Passo 3
Quando o valor de diminui gradativamente, mais corrente pode passar pela bobina e quanto mais corrente mais campo magnético sendo gerado para a direita. Para se opor a esse movimento a bobina vai requerer um campo magnético que aponte para a esquerda e para fazer isso a corrente induzida vai estar no sentido anti-horário na circuito onde a bobina está, ou seja ela vai passar de para .