Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 74
Um bloco de gelo de desliza para baixo em um plano inclinado sem atrito de de comprimento e de altura. Um operário empurra o bloco para cima com uma força paralela ao plano inclinado, fazendo o bloco descer com velocidade constante. (a) Determine o módulo da força exercida pelo operário. Qual é o trabalho realizado sobre o bloco (b) pela força do operário, (c) pela força gravitacional, (d) pela força normal do plano inclinado e (e) pela força resultante?
Passo 1
Vamos iniciar esta questão fazendo o DCL do bloco:
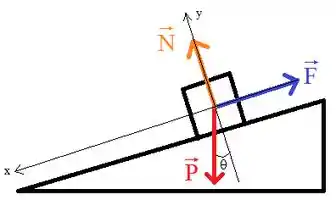
Portanto, aplicando a segunda lei de Newton ao eixo , lembrando que como o bloco se movimenta com velocidade constante, então:
Isolando :
Passo 2
Lembrando que, como ele deu o comprimento e a altura, devemos lembrar da relação trigonométrica que diz:
E usando o teorema de Pitágoras, temos:
Assim:
Passo 3
Com o valor do calculado, podemos usar a para determinar o valor da força que o operário deve fazer sobre o bloco de gelo:
Passo 4
Para calcular o trabalho de cada força do problema, como todas são constantes, então podemos usar a seguinte relação:
Assim, calculando o trabalho da força do operário, lembrando que a força atua no sentido contrário ao movimento, então . Então:
Passo 5
Para calcular o trabalho da força peso, devemos perceber que , então, para determinar usaremos o valor do calculado nos passos anteriores:
Assim:
E o trabalho do peso, portanto:
Passo 6
Agora, podemos determinar o trabalho da normal sabendo que ela atua na direção perpendicular ao movimento, assim, e . Então:
Passo 7
Como o bloco possui velocidade constante, então a força resultante sobre ele é nula, então:
Resposta
- ;
- ;
- ;
- ;
- .