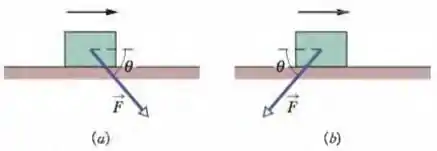
Na Fig. 7-47a, uma força de , que faz um ângulo para baixo e para a direita com a horizontal, é aplicada a um bloco de enquanto o bloco desliza para a dieita em um piso horizontal sem atrito. Escreva uma expressão para a velocidade do bloco após ser percorrida essa distância, para uma velocidade inicial de (a) e (b) para a direita. (c) A situação da Fig.7-47b é semelhante à do item (b), pois o bloco está inicialmente se deslocando para a direita com uma velocidade de , mas agora a força de está dirigida para baixo e para a esquerda. Escreva uma expressão para a velocidade do bloco após ser percorrida uma distância de . (d) Plote as três expressões de em função do ângulo , de a . Interprete os gráficos.

Como a aceleração é constante, então podemos usar a famosa equação de Torricelli para determinar a velocidade:

Considerando :

Substituindo os valores dados:

Agora, de maneira análoga para :

Substituindo os valores conhecidos:

Para a situação que o bloco está se movimentando com velocidade para direita e o corpo está sendo acelerado para esquerda, o que muda é o sentido da aceleração, então:

Substituindo os valores:

Vamos usar uma ferramenta para desenhar o gráfico das três situações, porém, o que devemos ter em mente:

Para o primeiro caso (): O valor do cosseno máximo ocorre em e, portanto, a velocidade máxima da corpo será . Porém, a medida que o ângulo cresce, diminui até zerar em .

Para o segundo caso (): O valor máximo da velocidade também ocorrerá quando , pois o cosseno é máximo. A velocidade máxima será . A medida que o ângulo cresce, a velocidade diminui, até chegar em quando o .

Para o terceiro caso (): Inicialmente, quando , a velocidade é nula, a medida que for crescendo, a velocidade atinge seu valor máximo em , quando .

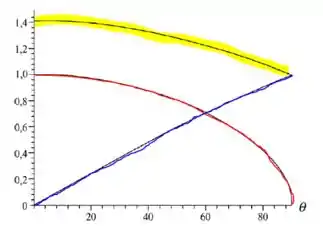
O gráfico vermelho representa o primeiro caso; O gráfico amarelo representa o segundo caso; O gráfico azul representa o terceiro caso.