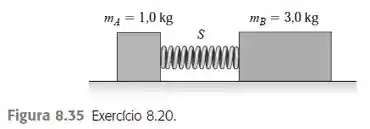
O bloco indicado na Figura possui massa igual a , e o bloco possui massa igual a . Os dois blocos se aproximam, comprimindo a mola entre eles; a seguir, o sistema é libertado a partir do repouso sobre uma superfície horizontal sem atrito. A mola possui massa desprezível, não está presa a nenhum dos blocos e cai sobre a mesa depois que se expande. O bloco adquire uma velocidade de .

a) Qual a velocidade final do bloco ?

b) Qual foi a energia potencial armazenada na mola comprimida?

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente calcular a velocidade final do bloco e a energia potencial armazenada na mola comprimida no sistema.

Nós sabemos que a massa do primeiro bloco é , que a massa do outro é , que os dois blocos se aproximam comprimindo a mola e que a velocidade do bloco é .

Sendo assim, pra calcular a velocidade do bloco (), vamos usar o princípio da conservação do momento linear, ou seja,

Onde é o momento linear inicial e é o momento linear final. Além disso, como o sistema parte do repouso, o momento inicial é zero (). Então, sabendo que é a soma dos momentos de cada bloco e que o momento é dado pelo produto da massa pela velocida, basta substituir os valores do enunciado.

Depois, pra calcular a energia potencial armazenada na mola, vamos usar a fórmula:

Vamos lá!