Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.3 - Ex. 21
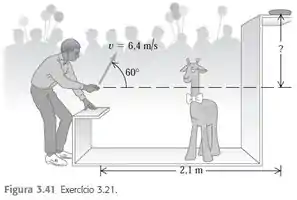
Em um parque de diversões você pode ganhar uma girafa inflável, se conseguir encaixar uma moeda de centavos em um prato pequeno. O prato está sobre uma prateleira acima do ponto em que a moeda deixa sua mão, a uma distância horizontal de deste ponto (Figura ). Se você lança a moeda com velocidade de formando um ângulo de acima da horizontal, a moeda se encaixa no prato. Despreze a resistência do ar. a) Qual a altura da prateleira em relação ao nível da sua mão? b) Qual é o componente vertical da velocidade da moeda imediatamente antes de a moeda pousar no prato?
Passo 1
Fala galera, tudo certo? Vamo que vamos. Eu sei que essa figura do livro é linda:
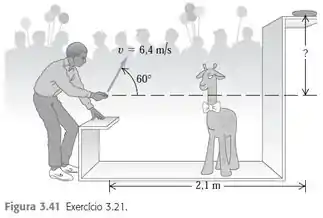
Mas pra gente ver melhor as coisas, vamos usar essa, que resume todas as nossas informações:
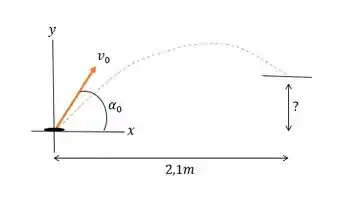
Como é uma questão de lançamento oblíquo, um bom primeiro passo é a gente descrever os movimentos na vertical e na horizontal. Em termos de aceleração, como só a gravidade atua nesse sistema, vamos ter:
Então podemos pegar a fórmula:
E separar ela pra cada um dos eixos:
Daqui em diante a gente vai olhar pros nossos dados e aos poucos ir inserindo eles nessas equações! Bora lá
Passo 2
Nesse movimento galera, inicialmente estamos na origem do nosso sistema de coordenadas! Oras, então o ponto inicial será . Nossas equações se tornam:
Sabemos as posições finais também! No eixo horizontal, é dado do enunciado! São os da imagem. No eixo vertical, é exatamente a altura que o projétil alcança! Considerando , vamos ter:
Podemos decompor o vetor velocidade inicial! Considerando o ângulo , que é um dado do enunciado, decompomos e calculamos as componentes dessa velocidade assim ó:
E logo:
Galera linda, temos um sistema de equações com tudo que precisamos! Mexendo na primeira, achamos:
Inserindo isso na segunda equação, temos:
E calculando, temos:
E ta na mão! A altura é de aproximadamente:
Tranquilo até aqui?
Passo 3
A letra nos pergunta qual é o componente vertical da velocidade da moeda imediatamente antes de a moeda pousar no prato. Pra isso, podemos usar a seguinte fórmula:
Nela, temos que:
E só pra lembrar, esses dados vieram, respectivamente:
- Decomposição da velocidade inicial; meio do Passo ;
- Condição inicial comentada no passo ;
- Tempo de duração do movimento todo; calculado no final do Passo .
Show, bora substituir:
Nem se preocupa com o sinal de negativo, ele só indica mesmo que a componente final do vetor velocidade aponta pra baixo ao invés de pra cima :D
E aí! entendeu tudo? Responde Aí! 👀
