Exercícios de Conservação do Momento Linear - Lista de Exercícios Resolvida
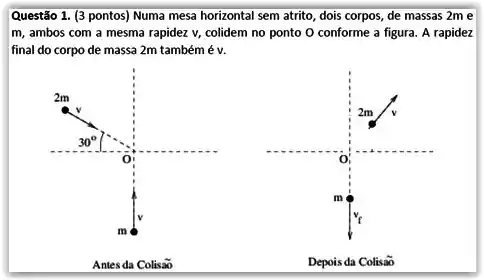
Questão 1
Uma partícula de momento , projétil, colide não frontalmente, isto é, colide bidimensionalmente, com uma outra partícula, inicialmente em repouso, que chamamos de alvo. Após a colisão o projétil tem momento e o alvo sai com momento . A conservação do momento linear, neste processo é corretamente representado pelo diagrama:
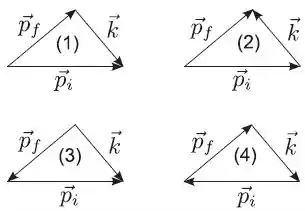
Nenhum diagrama está correto
Ver solução completaQuestão 2
Um bloco inicialmente em repouso explode em dois pedaços que entram em regiões com atrito onde terminam parando. O primeiro pedaço possui massa de 2 kg se move para a esquerda até parar após percorrer uma distância de 0, 15 m. O segundo pedaço se move para a direita e pára após percorrer uma distância de 0, 25 m. Sabendo que os coeficientes de atrito nas duas regiões são iguais, a massa total do bloco vale aproximadamente:
Ver solução completa
Questão 3
João e José estão sentados em um trenó que está inicialmente em repouso sobre uma superfície de gelo sem atrito. O peso de João é igual a , o peso de José é igual a e o peso do trenó é igual a . Ao notar a presença de uma aranha venenosa no interior do trenó eles imediatamente pulam para fora. João pula para a esquerda com velocidade (em relação ao gelo) igual a formando um ângulo de acima da horizontal, e José pula para direita com velocidade (em relação ao gelo) igual a formando um ângulo de acima da horizontal. Determine o módulo, a direção e o sentido da velocidade do trenó depois que eles pulam para fora.
Ver solução completaQuestão 4
Você está em pé sobre uma camada de gelo de um estádio de futebol em um país frio: despreze o atrito entre seus pés e o gelo. Um amigo joga para você uma bola de 0,400 kg que se desloca horizontalmente com velocidade de . Sua massa é igual a . Se você agarra a bola, com que velocidade você e a bola se deslocarão logo a seguir? Se a bola colide com você e rebate em seu peito, passando a adquirir uma velocidade horizontal de em sentido oposto ao inicial, com que velocidade você se desloca após a colisão?
Ver solução completaQuestão 5
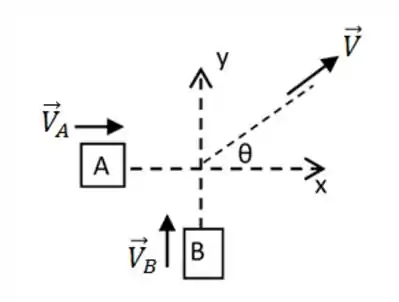
Dois automóveis viajam em duas estradas perpendiculares entre si, colidem e ficam juntos após a colisão. O carro tem massa de e tinha velocidade de antes da colisão. O carro tem massa de . As marcas de derrapagem dos carros juntos, imediatamente após a colisão fazem um ângulo de com a direção inicial do carro . Qual era a velocidade do carro antes da colisão?
Questão 6
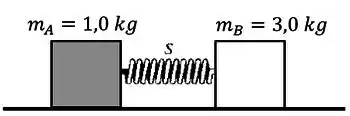
O bloco indicado na figura abaixo possui massa igual a , e o bloco possui massa igual a . Os dois blocos se aproximam, comprimindo a mola entre eles; a seguir o sistema é libertado a partir do repouso sobre uma superfície horizontal sem atrito. A mola possui massa desprezível, não está presa a nenhum dos blocos e cai sobre a mesa depois que ela se expande. O bloco adquire uma velocidade de . Qual a velocidade final do bloco ? Qual foi a energia potencial armazenada na mola comprimida?
Questão 7
Vamos supor que duas partículas e colidem bidimensionalmente. Seja a partícula de massa e a partícula de massa . As posições das partículas num certo instante antes da colisão são dadas por e . O tempo de duração da colisão é de .
Suponha agora que as velocidades no início da colisão são: e , e que no fim da colisão a componente da velocidade de é igual a e a componente da velocidade de é . Escreva os vetores velocidade de ambas as partículas no fim da colisão.
Ver solução completaQuestão 8
Um carrinho de massa move-se em linha reta sobre um piso horizontal sem atrito com velocidade de . Sobre o carrinho encontra-se fixada na posição horizontal, uma mola que é comprimida por um bloco de massa . Inicialmente, o bloco se encontra preso ao carrinho por um fio comprimindo a mola. Em certo instante, o fio se rompe e a mola empurra o bloco para fora do carrinho, projetando-o com uma velocidade de em relação ao piso. Uma vez livre do bloco, qual a nova velocidade do carrinho?
Ver solução completa
Questão 9
Uma nave viaja no espaço com vetor velocidade relativa a um observador, contendo uma carga. A massa total do sistema é . Em certo momento a nave libera a carga (massa ) com vetor velocidade relativa ao mesmo observador. Encontre uma expressão para o novo vetor velocidade da nave se durante a liberação da carga.
Ver solução completaQuestão 10
Uma granada encontra-se em repouso sobre uma mesa horizontal lisa (sem atrito) e explode em três fragmentos. Os fragmentos adquirem momentos lineares , e de módulos diferentes de zero, cuja direções formam ângulos diferentes entre si. O diagrama correto que representa a relação entre os momentos lineares deste fragmentos é
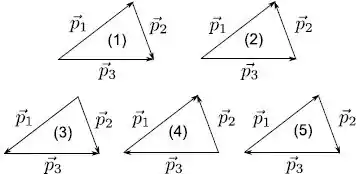
Questão 11
Um trenó de massa move-se horizontalmente com velocidade constante em um lago congelado. Ao passar por baixo de um viaduto, cai sobre ele verticalmente, um pacote de massa ficando preso a ele. O atrito entre as superfícies do lago e o trenó pode ser desprezado. Ao comparar-se, o momento linear, a velocidade, e a energia cinética do sistema trenó-pacote após o pacote cair sobre o trenó, é correto afirmar que:
- aumenta, diminui e aumenta;
- aumenta, permanece constante e aumenta;
- Diminui, diminui e diminui;
- permanece constante, permanece constante e permanece constante;
- permanece constante, diminui e diminui;
Questão 12
Uma partícula de momento , projétil, colide não frontalmente, isto é, colide bidimensionalmente, com uma outra partícula, inicialmente em repouso, que chamamos de alvo. Após a colisão o projétil tem momento e o alvo sai com momento . A conservação do momento linear, neste processo é corretamente representado pelo diagrama:
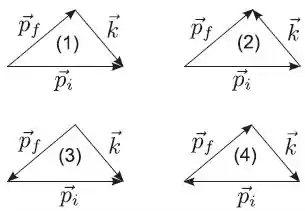
- Nenhum diagrama está correto
Questão 13
Duas partículas e de massas iguais colidem unidimensionalmente ao longo do eixo . Os gráficos a seguir representam as velocidades em função do tempo para cada partícula. Se é o momento linear do sistema formado pelas duas partículas e sua energia cinética, podemos afirmar que nessa colisão
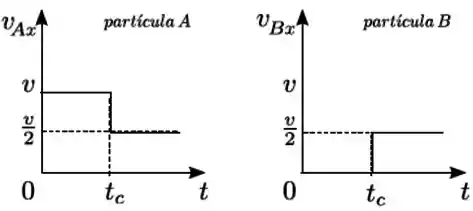
(a) se conserva e não se conserva
(b) se conserva e se conserva
(c) não se conserva e não se conserva
(d) não se conserva e se conserva
(e) e
Ver solução completaQuestão 14
Uma nave viaja no espaço com vetor velocidade relativa a um observador, contendo uma carga. A massa total do sistema é . Em certo momento a nave libera a carga (massa ) com vetor velocidade relativa ao mesmo observador. Encontre uma expressão para o novo vetor velocidade da nave se durante a liberação da carga.
Ver solução completaQuestão 15
Um homem de está em uma carroça de g que se move a . O homem pula da carroça e chega ao chão sem velocidade horizontal. A variação da velocidade da carroça é:
- Zero.
Questão 16
Um homem de se desloca no interior de um barco de com uma velocidade de em relação ao barco. O barco se encontra na superfície de um lago calmo e o atrito entre o barco e a água é desprezível. Admitindo que, após , o homem para e ainda se encontra no interior do barco, o deslocamento do barco medido em relação à margem vale:
- Nenhuma das outras alternativas.
Questão 17
A bala de um rifle de ar é disparada horizontalmente e fica alojada dentro um bola feita com massa de modelar suspensa por um fio vertical. O sistema bola + bala sobe até uma altura vertical de . Qual é a velocidade inicial da bala, dado que a sua massa é de e a massa da bola é de.
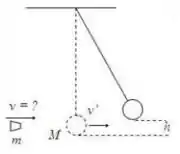
- Nenhuma das anteriores.
Questão 18
Um veículo da Ford, tipo Escort, cuja massa é , colide com um veículo de entrega, também da Ford, mas cuja massa é . A colisão acontece em um ângulo reto quando atravessam um cruzamento durante uma tempestade de neve, e a velocidade de ambos os veículos quando entram nesse cruzamento são iguais. Desprezando a força de atrito, qual a trajetória possível de ambos os veículos após a colisão?(admita que os veículos se mantenham preso um ao outro após a colisão).
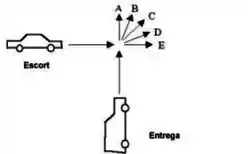
- Trajetória
- Trajetória
- Trajetória
- Trajetória
- Trajetória
Questão 19
Dois veículos espaciais em órbita estão acoplados e viajam a . A massa de um deles é de e a do outro . Para separá-los, é detonada entre os dois uma pequena carga explosiva que comunica uma energia cinética de ao conjunto dos dois veículos, medida em relação ao centro de massa do sistema. A velocidade relativa de afastamento um do outro é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 20
[ENUNCIADO COMUM ÀS QUESTÕES 4 e 5 do 2°EE 2017.2]
Duas partículas (A e B) estão sobre uma mesa horizontal sem atrito (plano ) e colidem num dado instante. Considere que representa a direção perpendicular à mesa.
[Questão 4]
Analise as afirmações a seguir sobre o sistema formado pelas partículas A e B.
(I) O momento linear total do sistema no plano se conserva porque não há forças externas ao longo das direções e .
(II) O momento linear total do sistema no plano não se conserva porque o somatório das forças externas ao longo das direçõesé nulo.
(III) O momento linear total do sistema no plano se conserva porque há forças externas ao longo das direçõesé, mas o seu somatório é nulo.
(IV) O momento linear total do sistema ao longo de se conserva porque não há forças externas nessa direção.
(V) O momento linear total do sistema ao longo de se conserva porque há forças externas nessa direção, mas o seu somatório é nulo.
(VI) O momento linear total do sistema ao longo de não se conserva porque o somatório das forças externas ao longo dessa direção não é nulo.
Estão corretas somente:
(a) I e IV
(b) I e V
(c) I e VI
(d) II e IV
(e) II e V
(f) II e VI
(g) III e IV
(h) III e V
(i) III e VI
Ver solução completaQuestão 21
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
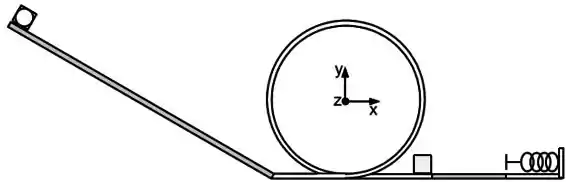
f) Os cubos colidem de forma perfeitamente inelástica. Sabendo que a colisão durou calcule a força feita no cubo em repouso. Suponha a velocidade do cubo imediatamente antes da colisão é de .
Ver solução completaQuestão 22
Um disco que hóquei de move-se sobre uma superfície horizontal com gelo e sem atrito. No instante t = 0, o disco de hóquei se move da esquerda para a direita a .
b) Se, em vez disso, fosse aplicada uma força de de a da direita para a esquerda, qual seria a velocidade final do disco de hóquei?
Ver solução completaQuestão 23
Um disco de hóquei de move-se sobre uma superfície horizontal com gelo e sem atrito. No instante , o disco de hóquei se move da esquerda para a direita a .
a) Determine o módulo, a direção e o sentido da velocidade do disco de hóquei após ele ter sofrido a ação de uma força de aplicada durante da esquerda para a direita.
Ver solução completaQuestão 25
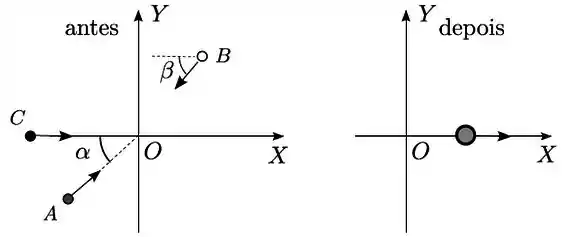
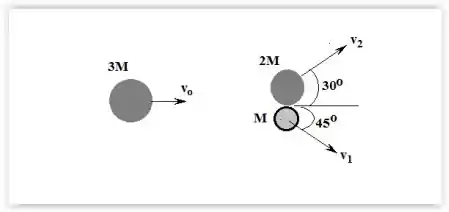
Três partículas , e , deslizando sobre uma mesa horizontal sem atrito, se aproximam da origem de um sistema de eixos no plano da mesa. Todas as três partículas atingem a origem simultaneamente e permanecem unidas após a colisão, sem perder contato com a mesa, deslocando-se ao longo do eixo no sentido positivo com velocidade de módulo desconhecida. As partículas , e têm massas respectivas , e , onde é uma constante conhecida. Antes da colisão as partículas têm velocidades de módulos respectivos , e , onde é uma constante conhecida. A partícula tem velocidade na direção e sentido do eixo e a partícula tem velocidade com direção e sentido indicados na figura por meio do ângulo conhecido . A velocidade da partícula tem o sentido indicado na figura mas sua direção é desconhecida e indicada pelo ângulo a ser determinado. Calcule
- O ângulo ;
- O módulo da velocidade após a colisão em função de ;
- A variação da energia cinética do sistema formado pelas três partículas no processo de colisão.
Questão 26
Um corpo de massa , movendo-se no sentido positivo X a uma rapidez , se rompe em duas partes cujas massas são , como é mostrado na figura.
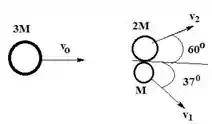
As velocidades escalares finais das partes em função de são, respectivamente,
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 27
Um corpo de massa , movendo-se no sentido positivo do eixo-x a uma velocidade , se rompe em duas partes cujas massas são e , conforme mostrado na figura. Determine as rapidezes finais das partes em função de .
- ;
- ;
- ;
- ;
- ;
Questão 28
Duas partículas de masssas e se deslocam sobre uma mesa horizontal sem atrito com velocidades iniciais de mesmo módulo . Elas possuem velocidades em direções perpendiculares e, em um dado instante, colidem e passam a se movimentar juntas. Qual o
módulo da velocidade com que elas se movimentam após a colisão?
a)
b)
c)
d)
e)
Ver solução completaQuestão 29
Duas lontras brincalhonas deslizam ao encontro uma da outra sobre uma superfície horizontal lamacenta (e, portanto, sem atrito). Uma delas, com massa de 7,50 kg, desliza para a esquerda a 5,00 m/s, enquanto a outra, com massa de 5,75 kg, escorrega para a direita a 6,00 m/s. Elas se agarram firmemente após colidirem.
(a) Ache o módulo, a direção e o sentido da velocidade dessas lontras logo após a colisão.
Ver solução completaQuestão 30
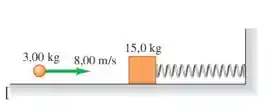
Um bloco de 15,0 kg é preso a uma mola horizontal muito leve com constante de força 500,0 N/m e está apoiado sobre uma mesa horizontal sem atrito (Figura). De repente, o bloco é atingido por uma pedra de 3,00 kg seguindo na horizontal a 8,00 m/s para a direita, quando a pedra recua a 2,00 m/s horizontalmente para a esquerda. Determine a distância máxima que o bloco comprimirá a mola após a colisão.
Questão 31
Uma bola de gude de 10,0 g desloca-se com velocidade de 0,400 m/s para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com outra bola de gude de 30,0 g que se desloca com velocidade de 0,200 m/s para a direita (Figura).
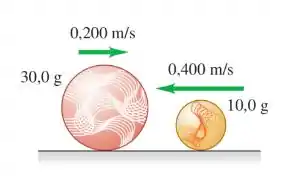
(a) Determine o módulo, a direção e o sentido de cada bola depois da colisão. (Como a colisão é frontal, todos os movimentos ocorrem ao longo da mesma linha.)
Ver solução completaQuestão 32
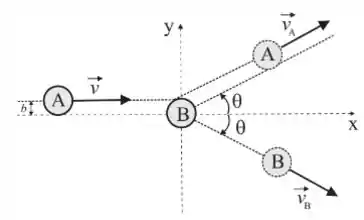
Um corpo de massa m incide com velocidade v sobre um outro corpo igual, com um parâmetro de colisão b, como mostrado na figura. Após a colisão, os dois corpos se afastam, formando um ângulo 2θ. Para , o módulo da variação da energia cinética de translação (∆T), em função da energia cinética inicial e do ângulo θ vale:
Questão 33
Num circo um acrobata está balançando no trapézio. Em uma determinada acrobacia
ele começa do repouso, fazendo um ângulo de 53◦ com a vertical, e no ponto inferior do movimento ele segura um outro acrobata, levando-o consigo no restante do movimento. Se o segundo acrobata tem massa , e o ângulo máximo com a vertical que eles atingem juntos é de 37◦, a massa do primeiro acrobata é:
considere cos53=0,6 e cos37=0,8.
a)
b)
c)
d)
e)
Ver solução completaQuestão 35
Um pendulo simples se encontra em repouso em sua posição de equilíbrio. Considere o fio ideal. Um pedaço de slime (uma tipo de massa que pode se deformar e grudar em outros objeto) com uma velocidade apenas com componente horizontal se desloca livremente até colidir com o pendulo, e a partir deste instante o sistema pendulo-slime passa a oscilar em torno de sua posição de equilíbrio. A massa do pendulo vale 0,05 kg e a massa de slime vale 0,03kg. O vetor velocidade do slime antes da colisão é de 4,0 i m/s.
- Determine o vetor velocidade do sistema slime-pendulo imediatamente após a colisão
- Determine a altura máxima que o pendulo irá atingir, tomando como referência a posição em que a massa se encontra no ponto de equilibrio
- Determine a variação de energia cinética do sistema slime-pendulo entre os instantes imediatamente antes da colisão e imediatamente após a colisão
- Determine o vetor Impulso sofrido pelo pêndulo devido a colisão.
Questão 36
A figura mostra os blocos e que estão sobre uma superfície horizontal sem atrito. Use os dados do quadro do lado onde são respectivamente as posições dos blocos e do centro de massa do sistema. No instante ilustrado(, são respectivamente as velocidades imediatamente antes da colisão dos corpos . Considerando a colisão entre os blocos unidimensional, determine:
Dados:
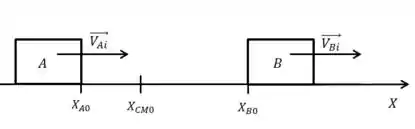
- O momento linear do sistema imediatamente após a colisão.
- A velocidade do centro de massa do sistema.
- O impulso do bloco transmitido pelo bloco sabendo que a velocidade imediatamente após a colisão de é igual a metade da velocidade imediatamente após a colisão de
Questão 37
Uma nave espacial de massa viaja com velocidade constante pelo espaço, sem interagir com qualquer outro corpo celeste. Num dado instante, ela explode, partindo-se em dois pedaços. O primeiro pedaço, de massa , passa a deslocar-se com velocidade constante. O segundo pedaço, de massa , passa a deslocar-se com velocidade constante . Todas as respostas abaixo devem ser escritas em termos de e .
(a) Calcule o vetor velocidade (expresso em termos dos vetores unitários e ).
(b) Qual é a velocidade do centro de massa do sistema após a explosão? Calcule ou justifique sua resposta.
(c) Calcule a variação da energia mecânica devida à explosão.
Ver solução completaQuestão 38
Enunciado das questões (Q4) e (Q5).
O sistema representado ao lado, formado por duas partículas de massas e , ligadas por uma haste em forma de gancho, de massa desprezível e comprimento , pode deslizar sem atrito sobre o plano horizontal . Uma terceira partícula, de massa , movendo-se sobre o plano com velocidade , colide com o sistema formado pelas partículas e , inicialmente parado, ficando presa no gancho.
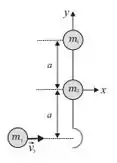
(Q4) [1,0 ponto] A velocidade de translação do sistema depois da colisão é:
Questão 39
6. Um pequeno drone está navegando numa dada altura constante quando, por causa de um defeito de fabricação, explode em dois fragmentos. Imediatamente após a explosão, verifica-se que um dos fragmentos com massa , move-se com velocidade e o outro fragmento, de massa , move-se com velocidade , ambas velocidades medidas no mesmo referencial inercial em repouso. A velocidade escalar do drone antes da explosão, em metros por segundo, medida no mesmo referencial inercial é:
Ver solução completaQuestão 40
Dois blocos, de massas M = 3,0 kg e m = 1,0 kg, são inicialmente mantidos em repouso sobre uma superfície horizontal, comprimindo uma mola ideal. Ao serem simultaneamente liberados da mola, cada bloco viaja para um lado e sobe uma rampa inclinada. Considere que a velocidade do bloco de massa M logo após ser liberado é V = 3,0 m/s. Despreze todos os atritos e use
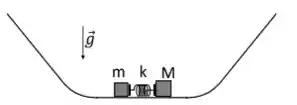
Qual é o módulo da velocidade (em m/s) do bloco de massa m logo após os blocos serem liberados?
a) 1,0
b) 3,0
c) 4,0
d) 5,0
e) 6,0
f) 7,0
g) 8,0
h) 9,0
Ver solução completaQuestão 41
Um bloco de massa é lançado, a partir do repouso, ao longo de uma rampa sem atrito de um ponto situado a uma altura do plano horizontal, como esquematizado na figura abaixo. Ao final da rampa, o bloco colide com o bloco de massa , inicialmente em repouso próximo ao ponto . A colisão é completamente inelástica. Após o ponto há um trecho da pista horizontal (região hachurada na figura a partir do ponto ) cujo coeficiente de atrito cinético é . Considere .
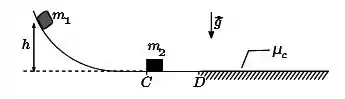
(a) Calcule o módulo da velocidade do bloco imediatamente antes da colisão.
(b) Determine as velocidades dos blocos imediatamente após a colisão. Baseado em qual princ´ıpio de conservação é possível encontrar esse resultado?
(c) Ao percorrer o trecho com atrito os blocos inevitavelmente param. Calcule a distncia percorrida pelos blocos nesse trecho a partir do ponto até que fiquem em repouso.
(d) Calcule a razão entre o trabalho realizado pela força de atrito sobre os blocos até que fiquem em repouso e a energia cinética inicial perdida durante a colisão .
Ver solução completaQuestão 42
A figura mostra um besouro parado na extremidade direita de um carrinho em repouso sobre uma superfície horizontal. O besouro e o carrinho tem massas de e , respectivamente. Se não há atrito entre o carrinho e a superfície, que velocidade o carrinho adquire quando o besouro se movimenta para a esquerda com velocidade de módulo ?
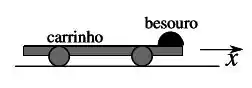
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 43
Um projétil de massa é disparado com velocidade horizontal contra um bloco de massa , inicialmente em repouso sobre uma mesa horizontal com atrito desprezível. Se o projétil atravessa o bloco e tem sua velocidade final igual a , o módulo da velocidade adquirida pelo bloco é
a)
b)
c)
d)
e)
Ver solução completaQuestão 44
Em um experimento de colisão nuclear, mediu-se o espalhamento de partículas , de massa e velocidade inicial , após elas colidirem com núcleos de ouro em repouso e de massa . Sabe-se que as forças externas são desprezíveis. Se a velocidade da partícula medida após a colisão é , pode-se afirmar que:
a) a velocidade do núcleo de ouro após a colisão é
b) a velocidade do núcleo de ouro após a colisão é
c) a velocidade do núcleo de ouro após a colisão é
d) a velocidade do núcleo de ouro após a colisão é
e) a velocidade do núcleo de ouro após a colisão é
Ver solução completaQuestão 45
Um sapo está, inicialmente, situado num dos extremos de uma plataforma de comprimento que flutua, em repouso, sobre as águas paradas de um lago. Num dado instante, o sapo dá um salto com uma velocidade de módulo e que faz com a horizontal um ângulo como mostra a figura. Suponha que a plataforma se movimente apenas na horizontal e despreze o atrito entre a água e a plataforma. Seja a massa do sapo e a massa da plataforma. Após o sapo pular, pode-se afirmar que:
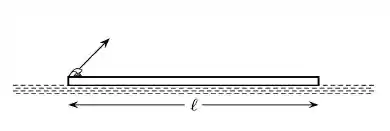
a) a plataforma se move para esquerda com velocidade de módulo
b) a plataforma se move para esquerda com velocidade de módulo
c) a plataforma se move para direita com velocidade de módulo
d) a plataforma se move para esquerda com velocidade de módulo
e) a plataforma se move para esquerda com velocidade de módulo
f) a plataforma não se move
Ver solução completaQuestão 46
Um corpo de massa move-se na direção positiva do eixo x com velocidade inicial . Uma explosão interna de curta duração divide o corpo em três pedaços. Imediatamente após a explosão, um dos fragmentos, com massa , afasta-se do local da explosão com velocidade ao longo do eixo y positivo. Um segundo fragmento, com massa , tem velocidade de módulo na direção x negativa.
- Determine a velocidade do terceiro fragmento. Escreva sua expressão em termos dos vetores unitários nas direções x e y. Calcule seu módulo.
- Calcule a quantidade de energia liberada na explosão.
Questão 47
Uma bola com momento quica no chão sem perder energia cinética. Qual é a variação de momento da bola a cada quicada?
a)
b)
c)
d)
e)
Ver solução completaQuestão 48
Dois caminhões de massa , com velocidades , respectivamente, e trajetórias perpendiculares entre si, colidem em um cruzamento no ponto G e passam a se movimentar unidos até o ponto H, conforme a figura abaixo.
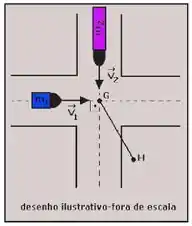
Considerando o choque perfeitamente inelástico, o módulo da velocidade dos veículos imediatamente após a colisão é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 49
Uma partícula de massa desloca-se sobre uma mesa horizontal, sem atrito, com velocidade de módulo . Num certo instante ela se desintegra espontaneamente em três fragmentos de massas , e como mostrado na figura. O módulo da velocidade do fragmento de massa é igual àquele de massa , ao passo que o fragmento de massa segue a mesma direção e sentido da velocidade original da partícula.
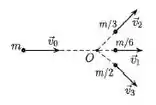
Qual das quantidades associadas ao sistema de massa a seguir não se conserva no processo de desintegração?
(a) Energia cinética.
(b) Momento linear.
(c) Velocidade da posição do centro de massa.
(d) Momento angular em relação ao ponto O, onde ocorreu a desintegração.
(e) Massa total.
Ver solução completaQuestão 50
Um carro em uma estrada acelera do repouso por um determinado intervalo de tempo. Neste processo, o valor absoluto do momento linear do carro varia de um certo valor. Ignorando outros efeitos sobre a Terra, o que acontece com o momento linear da Terra devido ao movimento do carro?
a) varia de uma quantidade maior.
b) varia de mesma quantidade.
c) varia de uma quantidade menor.
d) não varia.
e) preciso de mais informações.
Ver solução completaQuestão 51
Um bloco de com uma velocidade escalar de colide com um bloco de com uma velocidade escalar de que se move na mesma direção e sentido. Após a colisão, o bloco de passa a se mover no mesmo sentido com uma velocidade de .
(a) Qual é a velocidade do bloco de imediatamente após a colisão?
(b) De quanto varia a energia cinética total do sistema dos dois blocos por causa da colisão?
(c) Suponha que a velocidade do bloco de após o choque é . Qual é, nesse caso, a variação da energia cinética total?
(d) Explique o resultado do item (c).
Ver solução completaQuestão 52
Um vaso inicialmente em repouso na origem de um sistema de coordenadas explode em três pedaços. Imediatamente após a explosão, um dos pedaços, de massa , se move com velocidade e um segundo pedaço, também de massa , se move com velocidade . O terceiro pedaço tem massa . Determine
(a) o módulo e
(b) a orientação da velocidade do terceiro pedaço logo após a explosão.
Ver solução completaQuestão 53
Um homem de em repouso em uma superfície horizontal de atrito desprezível arremessa uma pedra de com uma velocidade horizontal de . Qual é a velocidade do homem após o arremesso?
Ver solução completaQuestão 54
Um astronauta estava vagando em torno de uma estação espacial, sem uma corda que o prendesse a ela. Ele percebe que a estação se afasta dele com velocidade igual a . Ele tem em suas mãos uma ferramenta de massa igual . Para retornar a estação espacial, ele decide lançar a ferramenta na direção formada pela reta que liga ele à estação, mas em sentido oposto a ela, com uma dada velocidade de módulo . Se ele, o astronauta, só com sua roupa espacial (sem contar a ferramenta), tem massa igual a , determine que valor de velocidade ele deve imprimir à ferramenta, de modo que ele passe a se aproximar da estação com velocidade igual a .
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 55
Um patinador de massa , carregando uma bola de massa , vai em direção a uma parede com velocidade . Num dado instante, ele lança a bola perpendicularmente contra a parede, com velocidade em relação ao solo. Esta rebate na parede e volta nas mãos do patinador. Considere a colisão da bola com a parede perfeitamente elástica e despreze o atrito entre o piso e o patinador, assim como o efeito da gravidade sobre a trajetória da bola.
Qual é a velocidade do patinador após lançar a bola?
Qual é a velocidade do patinador após agarrar a bola rebatida pela parede?
Ver solução completaQuestão 56
O momento linear total de dois corpos que colidem entre si se conserva se e somente se:
(A) as massas dos dois corpos forem iguais.
(B) não há variação na rapidez das partículas colidentes.
(C) a resultante das forças externas for nula.
(D) a colisão for perfeitamente inelástica.
(E) os dois corpos colidentes tiverem a mesma rapidez inicial.
Ver solução completaQuestão 57
Num referencial inercial munido de um sistema de coordenadas cartesianas, um corpo de massa com velocidade inicial colide com um corpo de massa inicialmente em repouso. O corpo de massa passa então a se movimentar com velocidade . A partir desta descrição podemos afirmar que o corpo de massa possuirá uma velocidade final na forma:
A.
B.
C.
D.
E.
Ver solução completaQuestão 58
Dois veículos têm, num certo instante, quantidades de movimento de mesma intensidade. As massas dos veículos são e toneladas. Se o veículo de menor massa tem velocidade de , qual a velocidade do outro veículo?
Ver solução completaQuestão 60
Duas caixas, da massa e , estão presas através de uma mola que está comprimida e um fio e em repouso sobre um plano horizontal com atrito desprezível, como mostra a figura. Suponha que o fio seja cortado por uma pessoa e o bloco "" passe a deslizar com uma velocidade de . Nessas condições, podemos afirmar que a velocidade adquirida pelo bloco "" vale:
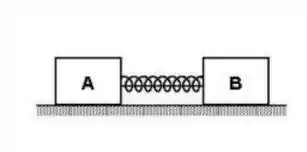
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 61
Dois objetos A e B colidem. O objeto A possui uma massa de 2,0 kg e o objeto B possui massa 3,0 kg. A velocidade de A antes da colisão é = 15î+ 30ĵ(m⁄s) e a velocidade de B antes da colisão é = −10î+ 5,0ĵ(m⁄s). Após a colisão a velocidade de A é = −6,0î+ 30ĵ(m⁄s). Qual é a velocidade final de B?
a) = 4,0î+ 5,0ĵ(m⁄s)
b) = 10î− 8,0ĵ(m⁄s)
c) = 2,0î− 10ĵ(m⁄s)
d) = 40î+ 7,0ĵ(m⁄s)
e) = −4,0î+ 15ĵ(m⁄s)
Ver solução completaQuestão 62
Na Figura 3, o bloco A de massa = 2,0 kg encontra-se inicialmente em repouso, preso a uma mola ideal comprimida de 0,10 m. A constante el ́astica da mola vale k = 40 N/m. Nos itens a seguir, considere g = e despreze todos os atritos. O bloco não perde o contato com a superfície.
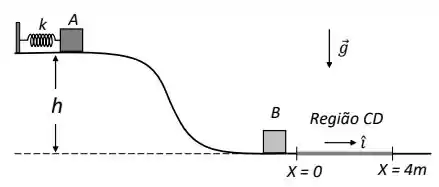
a) Calcule a velocidade do bloco ap ́os descer a rampa de altura h = 0,19 m em relação ao nível do solo.
b) Após descer a rampa, o bloco A sofre uma colisão perfeitamente inelástica com um bloco B de massa = 8,0 kg inicialmente em repouso. A colisão faz um bloco grudar no outro. Calcule a velocidade dos blocos imediatamente após a colisão.
c) Após a colisão, os blocos permanecem grudados e ingressam na região CD horizontal, com início na posição x = 0 e término em x = 4,0 m. Nessa região, os blocos estão sujeitos a força variável (em newtons), que os acelera para a frente, onde x é a posição dos blocos e é o vetor unitrio horizontal para a direita. Calcule o trabalho realizado por F entre as posições x = 0 e x = 4,0 m.
Sugestão: Faça o gráfico de F em função de x.
Ver solução completaQuestão 63
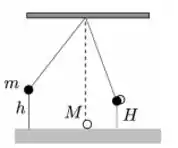
Uma massa m é pendurada por um fio ideal. Ela é abandonada da altura h a partir do repouso e colide com a massa M, também em repouso, de forma totalmente inelástica; vide a figura. Após a colisão a razão entre h e altura máxima H que ambas atingem é:
Questão 64
13 - Tempestades solares são causadas por um fluxo intenso de partículas de altas energias ejetadas pelo Sol durante erupções solares. Esses jatos de partículas podem transportar bilhões de toneladas de gás eletrizado em altas velocidades, que podem trazer riscos de danos aos satélites em torno da Terra. Considere que, em uma erupção solar em particular, um conjunto de partículas de massa total , deslocando-se com velocidade de módulo , choca-se com um satélite de massa que se desloca com velocidade de módulo igual a na mesma direção e em sentido contrário ao das partículas. Se a massa de partículas adere ao satélite após a colisão, o módulo da velocidade final do conjunto será de
A) .
B)
C)
D)
E)
Ver solução completaQuestão 67
Nos gráficos ao lado estão representadas possíveis trajetórias de colisão de duas partículas de mesma massa em um sistema isolado. Em cada gráfico as trajetórias são mostradas para o mesmo intervalo de tempo. As setas indicam o sentido do movimento em cada trajetória. Quais dos gráficos são compatíveis com trajetórias das partículas antes e depois de uma colisão?
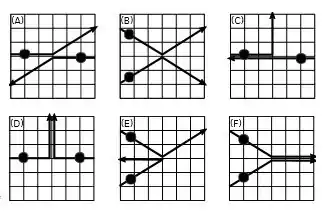
(a) A, B, C, D
(b) B, C, D
(c) A, B, D, E
(d) A, E, F
(e) B, C, F
(f) A, B, F
Ver solução completaQuestão 68
Um bloco inicialmente em repouso explode em dois pedaços que entram em regiões com atrito onde terminam parando. O primeiro pedaço possui massa de 2 kg se move para a esquerda até parar após percorrer uma distância de 0, 15 m. O segundo pedaço se move para a direita e pára após percorrer uma distância de 0, 25 m. Sabendo que os coeficientes de atrito nas duas regiões são iguais, a massa total do bloco vale aproximadamente:
a) M = 4, 6 kg
b) M = 2, 3 kg
c) M = 3, 5 kg
d) M = 4, 0 kg
e) M = 1, 7 kg
Ver solução completaQuestão 69
Um bloco de massa m e velocidade inicial v0 colide com outro bloco de massa desconhecida, inicialmente em repouso. Considerando uma colisão elástica unidimensional e sabendo que o bloco projétil de massa m recua após a colisão com uma velocidade de modulo –(1/3)v0, a massa do bloco alvo é:
a) desconhecida
b) 4m
c) 1m
d) 2m
e) 3m
Ver solução completaQuestão 70
Dois automóveis viajam em duas estradas perpendiculares entre si, colidem e ficam juntos após a colisão. O carro tem massa de e tinha velocidade de antes da colisão. O carro tem massa de . As marcas de derrapagem dos carros juntos, imediatamente após a colisão fazem um ângulo de com a direção inicial do carro . Qual era a velocidade do carro antes da colisão?
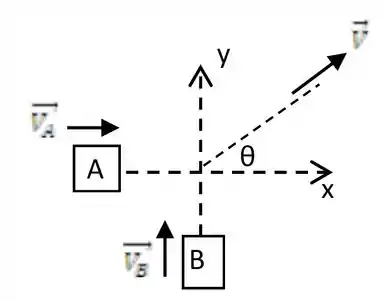
Questão 72
A figura mostra o resultado de uma colisão entre dois corpos de massas desiguais. Determine:
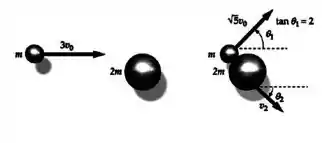
O ângulo
A rapidez da maior massa após a colisão.
Classifique a colisão quanto à variação de energia cinética, justificando sua resposta.
Ver solução completaQuestão 74
Um canhão dispara um projétil com uma velocidade inicial e um ângulo com a horizontal. No topo da trajetória, o projétil explode em dois fragmentos de massas iguais (figura abaixo). Um fragmento, cuja velocidade imediatamente após a colisão é zero, cai verticalmente. Suponha que o terreno é nivelado e despreze a resistência do ar. A que distância do canhão cai o outro fragmento?
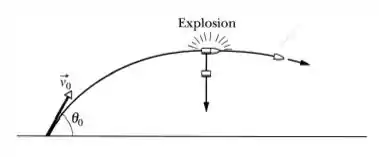
Questão 78
Uma bola cai no solo de uma altura h e retorna até a altura h'. O momento linear do sistema {bola-Terra} é conservado
(A) não importa a altura h' alcançada.
(B) somente se h'
(C) somente se h' = h.
(D) somente se h' > h.
(E) somente se h' h .
Ver solução completaQuestão 79
Dois carros idênticos colidem em três experimentos em um trilho sem atrito. Em cada caso, o carro A está inicialmente com velocidade e o carro está em repouso. Esquematize o gráfico velocidade tempo para cada carro
- Se os carros ficam grudados após a colisão
- Se o carro A é estacionário depois da colisão, e
- Se o carro A tem velocidade depois da colisão
- Interprete as colisões em cada caso.
Questão 80
Um projetil de está viajando para o leste com módulo de velocidade igual a quando de repente explode em 3 pedaços. Um fragmento da explosão, com massa de vai para o oeste a outro fragmento, também de , viaja a norte da velocidade inicial, com Dados:
- Qual a velocidade (módulo, direção e sentido) do terceiro fragmento?
- Qual a velocidade (módulo, direção e sentido) do centro de massa imediatamente após a explosão? Justifique a sua resposta.
- Calcule a energia liberada na explosão.
Questão 81
Dois corpos de massas iguais se deslocam em uma mesa horizontal sem atrito. Inicialmente eles possuem velocidades de mesmo módulo e o objeto de massa se desloca fazendo um ângulo com o eixo enquanto o de massa fazendo o mesmo ângulo , porém com o eixo , conforme a figura a seguir. Em um certo instante, os corpos colidem e passam a se deslocar juntos. O trabalho realizado pelas forças internas, que atuam durante a colisão, sobre o sistema será de:
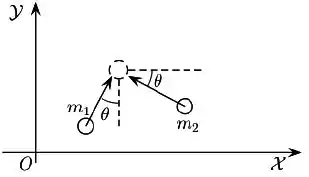
(a)
(b)
(c) O trabalho é nulo.
(d)
(e)
(f)
Ver solução completaQuestão 82
PARTE I
Uma bola de massa se move no sentido positivo do eixo x em um plano horizontal sem atrito com velocidade de valor . Ela colide com uma bola de massa em repouso. Após esse fato a bola passa a se mover com velocidade escalar no sentido negativo do eixo y. Desconhece-se se a colisão é elástica.
(a ) Obtenha o valor do ângulo que a velocidade final da bola A faz com o eixo x.
(b ) Encontre uma expressão literal para a velocidade escalar final da bola A em função de
PARTE II:
Um pêndulo em forma de bola com massa é largado de uma altura , conforme a figura ao lado, para colidir com outro pêndulo em repouso, constituído pela bola de massa . A colisão é frontal na direção horizontal de seus centros de massa e ocorre quando os dois estão na vertical. Pode-se desprezar a resistência do ar sobre os pêndulos durante a colisão.
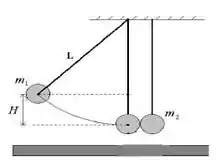
Coloque Verdadeiro (V) ou Falso (F) nas afirmações abaixo e as justifique com base em leis físicas.
1- A força resultante externa durante a colisão é nula sobre o sistema de dois pêndulos e o momento linear é conservado.
2- A componente horizontal do Momento linear do sistema se conserva durante a colisão.
Ver solução completaQuestão 83
A condição necessária para a conservação do momento linear de um sistema de partículas é que:
a) uma partícula esteja em repouso;
b) as forças internas se igualem às forças externas;
c) as forças internas não realizem trabalho;
d) a força externa resultante sobre o sistema seja zero;
e) a energia mecânica se conserve;
Ver solução completaQuestão 84
Uma esfera de massa é lançada em um trilho unidimensional de atrito desprezível com velocidade ao encontro de uma segunda esfera lançada simultaneamente de massa desconhecida com velocidade . As esferas colidem elasticamente e durante a colisão a primeira esfera sofre uma força dada pelo gráfico abaixo.
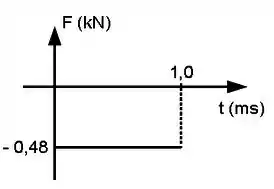
(a) Nesta colisão o momento linear do sistema (duas esferas) é conservado? Porque?
Ver solução completaQuestão 86
[ENUNCIADO COMUM ÀS QUESTÕES 4 e 5 do 2°EE 2017.2]
Duas partículas (A e B) estão sobre uma mesa horizontal sem atrito (plano ) e colidem num dado instante. Considere que representa a direção perpendicular à mesa.
[Questão 5]
As partículas A e B têm massas (a ser determinada) e . Antes da colisão, suas velocidades (em ) são e . Após a colisão, suas velocidades (em ) são e O valor de é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 87
Duas partículas colidem num plano horizontal e sem atrito. Antes da colisão, a partícula de massa tinha velocidade , enquanto que a partícula de massa tinha velocidade . Após a colisão, sai com velocidade . Qual é a velocidade final de ?
Questão 88
Um rojão de massa M explode após seu lançamento em apenas dois pedaços, um com o dobro da massa do outro. O rojão imediatamente antes da explosão tem velocidade e o pedaço de menor massa imediatamente após a explosão tem velocidade −2 . A velocidade do pedaço de maior massa imediatamente após a explosão é:
a)
b)
c)
d) 0
e)
Ver solução completaQuestão 90
Um objeto de massa é abandonada do repouso, em queda livre, atinge o solo horizontal com uma velocidade de módulo igual a . Imediatamente após a colisão a esfera tem uma velocidade vertical de módulo . O módulo da variação da quantidade de movimento da esfera, na colisão com o solo, em , é de:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 91
Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.
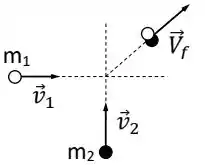
A variação da energia cinética total das massas, , devido a colisão é:
a) 0 J
b) −6,0 J
c) −3,0 J
d) −1,5 J
e) 1,5 J
f) 3,0 J
g) 6,0 J
h) 8,0 J
Ver solução completaQuestão 92
Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.
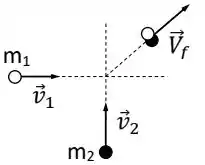
Considere as massas das partículas = 6,0 kg e = 4,0 kg, e suas respectivas velocidades antes da colisão e . A velocidade (em m/s) das partículas após a colisão é:
a)
b)
c)
d)
e)
f)
g)
h)
Ver solução completaQuestão 93
A figura ao lado é uma ilustração do pêndulo de Newton utilizando 5 esferas idênticas. Numa montagem com as alturas das esferas bem alinhadas entre si e corretamente posicionadas, verifica-se que o momentum e a energia são grandezas conservadas neste sistema. Inicialmente 3 esferas estão deslocadas a uma altura a com relação às respectivas posições de repouso (veja figura). Marque a opção CORRETA com relação ao que irá ocorrer após essas 3 esferas serem soltas:
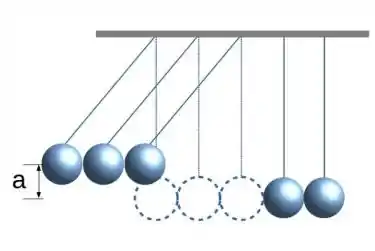
a) apenas a esfera mais a direita irá adquirir uma altura equivalente a 3a, enquanto as demais esferas permanecerão em repouso.
b) as 2 esferas mais a direita irão adquirir uma altura equivalente a 1,5a, enquanto as demais esferas permanecerão em repouso.
c) as 3 esferas mais a direita irão adquirir uma altura equivalente a 1a, enquanto as demais esferas permanecerão em repouso.
d) todas as 5 esferas irão adquirir uma altura equivalente a 3a/5.
e) não é possível prever o que irá ocorrer por falta de informações adicionais.
Ver solução completaQuestão 94
A lei de conservação de momento linear se aplica a um sistema de partículas que colidem entre si se e só se:
(A) a posição do centro de massa do sistema varia.
(B) não há variação na rapidez das partículas colidentes.
(C) o impulso da resultante das forças externas for nulo.
(D) a colisão for inelástica.
(E) a posição do centro de massa do sistema permanecer fixa.
Ver solução completaQuestão 95
Um aro rígido de raio e massa está deitado sobre uma mesa sem atrito e é articulado num ponto . Um objeto pontual de massa tem velocidade para a direita numa trajetória diametral de aro. Ele colide elasticamente com o aro. Depois da colisão, o objeto está retornando para a esquerda com velocidade e o aro passa a rodar com velocidade angular . O momento de inércia do aro por um eixo através do seu centro e perpendicular ao plano do aro é .
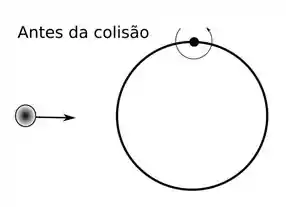
Qual é a velocidade do objeto depois da colisão? Expresse sua resposta em função das variáveis do exercício. Não use em sua resposta.
Ver solução completaQuestão 96
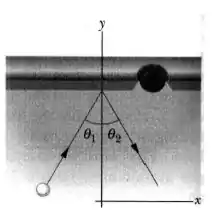
A figura abaixo dá uma vista superior da trajetória de uma bola de bilhar de quando ela bate na borda de uma mesa. O módulo da velocidade inicial é e o ângulo é . A rebatida inverte a componente da velocidade da bola, mas não altera a componente . Determine
(a) o ângulo e
(b) a variação do momento linear da bola em termos dos vetores unitários. (O fato de que a bola está rolando é irrelevante para a solução do problema.)
Questão 97
6) Uma partícula de massa colide com uma parede vertical fixa e lisa. A partícula incide com velocidade de módulo fazendo um ângulo com a parede e emerge também com velocidade de módulo fazendo um ângulo com a parede, como indica a figura.
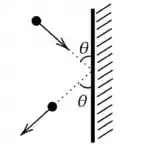
Sobre essa situação, são realizadas as seguintes afirmativas:
- Como a colisão é elástica, o impulso da parede sobre a partícula é nulo.
- Considerando o sistema formado somente pela partícula, apenas a componente horizontal do momento linear se conserva na colisão.
- A força média da parede sobre a partícula é horizontal.
São VERDADEIRAS apenas:
(a) III
(b) I
(c) Todas
(d) Nenhuma
(e) II
Ver solução completaQuestão 98
Um rojão, lançado segundo um ângulo de , explode em dois fragmentos ao atingir sua altura máxima, de m; os fragmentos são lançados horizontalmente. Um deles, de massa igual a , cai no mesmo plano vertical da trajetória inicial, a de distância do ponto de lançamento. O outro fragmento tem massa igual a .
(a) A que distância do ponto de lançamento cai o fragmento mais leve?
Ver solução completaQuestão 99
7) Uma partícula de massa colide com uma parede vertical fixa e lisa. A partícula incide com velocidade de módulo fazendo um ângulo com a parede e emerge também com velocidade de módulo fazendo um ângulo com a parede, como indica a figura.
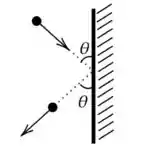
Sobre essa situação, são realizadas as seguintes afirmativas:
- Como a colisão é elástica, o impulso da parede sobre a partícula é nulo.
- Considerando o sistema formado somente pela partícula, apenas a componente horizontal do momento linear se conserva na colisão.
- A força média da parede sobre a partícula é horizontal.
São VERDADEIRAS apenas:
(a) III
(b) I
(c) Todas
(d) Nenhuma
(e) II
Ver solução completaQuestão 100
Um explosivo é colocado dentro de um objeto de massa M, que é lançado para o alto. No ponto mais alto da trajetória o objeto explode, partindo-se em três partes de massas M/2, M/4 e M/4. A parte mais pesada se desloca para cima com velocidade v, e uma das partes de massa M/4 se desloca para a esquerda com a mesma velocidade v. Qual a velocidade horizontal e vertical do terceiro pedaço?
a) v para a direita e 2v para baixo
b) v para a direita e v para baixo
c) 2v para a direita e v para baixo
d) 2v para a direita e 2v para baixo
e) depende da quantidade de energia fornecida pela explosão.
Ver solução completaQuestão 101
Um corpo de 3 kg escorrega ao longo de um plano horizontal sem atrito com velocidade . Num certo instante, explode, dividindo-se em duas partes, uma de massa 2 kg e outra de massa 1 kg. Depois da explosão, o pedaço de 1 kg desloca-se com velocidade .
a. Qual a velocidade do pedaço de 2 kg depois da explosão?
Ver solução completaQuestão 102
Um corpo de 3 kg escorrega ao longo de um plano horizontal sem atrito com velocidade . Num certo instante, explode, dividindo-se em duas partes, uma de massa 2 kg e outra de massa 1 kg. Depois da explosão, o pedaço de 1 kg desloca-se com velocidade .
b. Qual a velocidade do centro de massa depois da explosão?
Ver solução completaQuestão 103
Um projétil de 6 kg é disparado num ângulo com a horizontal, com velocidade inicial de 40 m/s. No topo da sua trajetória, o projétil explode em dois fragmentos com massas de 2 kg e 4 kg. Os fragmentos deslocam-se na horizontal, imediatamente depois da explosão, e o fragmento de 2 kg cai no lugar do disparo do projétil. Determine:
a. O local onde cai o fragmento de 4 kg;
Ver solução completaQuestão 104
Um projétil de 6 kg é disparado num ângulo com a horizontal, com velocidade inicial de 40 m/s. No topo da sua trajetória, o projétil explode em dois fragmentos com massas de 2 kg e 4 kg. Os fragmentos deslocam-se na horizontal, imediatamente depois da explosão, e o fragmento de 2 kg cai no lugar do disparo do projétil. Determine:
b. A energia liberada na explosão.
Ver solução completaQuestão 105
Um homem com 70 kg e um garoto de 35 kg, estão juntos sobre uma superfície gelada, na qual o atrito é desprezível. Um empurra o outro, e o homem se desloca para trás, com velocidade de 0, 3 m/s, em relação ao gelo.
a. Qual a separação dos dois depois de 5 s?
Ver solução completaQuestão 106
Um homem com 70 kg e um garoto de 35 kg, estão juntos sobre uma superfície gelada, na qual o atrito é desprezível. Um empurra o outro, e o homem se desloca para trás, com velocidade de 0, 3 m/s, em relação ao gelo.
b. A energia mecânica do sistema se conserva?
Ver solução completaQuestão 107
Um garoto de massa 30 kg, correndo a 2, 5 m/s, salta sobre um carrinho de massa 10 kg, que estava parado, permanecendo sobre ele.
a. Determine a velocidade do conjunto carrinho+garoto depois que ambos estiverem andando juntos.
Ver solução completaQuestão 108
Um garoto de massa 30 kg, correndo a 2, 5 m/s, salta sobre um carrinho de massa 10 kg, que estava parado, permanecendo sobre ele.
b. Em seguida, o garoto começa a andar sobre o carrinho com a velocidade de 0, 5 m/s, relativa ao carrinho, dirigindo-se para frente do mesmo. Qual a nova velocidade do carrinho?
Ver solução completaQuestão 109
Um garoto de massa 30 kg, correndo a 2, 5 m/s, salta sobre um carrinho de massa 10 kg, que estava parado, permanecendo sobre ele.
c. Quando o garoto chega na extremidade do carrinho, ele pula para frente com velocidade de 1 m/s em relação ao carrinho. Com que velocidade o carrinho fica depois disso?
Ver solução completaQuestão 110
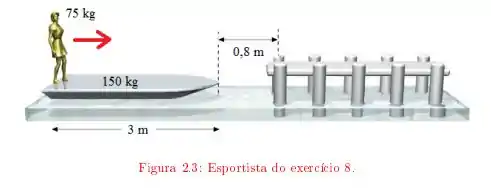
Uma esportista de 75 kg sentada na popa de uma canoa de 150 kg e 3 m de comprimento, conseguiu encostá-la em uma estaca, onde quer amarrar a canoa. Ao encostar a canoa, ela se levanta e caminha até atingir a outra extremidade, o que leva a canoa a afastar-se da margem. Ela consegue, esticando o braço, alcançar até uma distância de 80 cm da estaca. Conseguirá amarrar a canoa? Caso contrário, quanto falta? Despreze a resistência da água e considere o centro de massa da canoa como localizado em seu ponto médio.
Questão 111
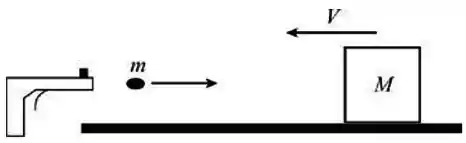
Um bloco de madeira de massa está se movendo a uma velocidade em uma linha reta. Qual a velocidade que a bala de massa precisa viajar para parar o bloco (suponha que a bala se aloja no interior)?
Questão 112
Uma bola de golfe é atirada contra uma bola de boliche inicialmente em repouso de massa 100 vezes maior. Como a colisão é elástica, ela volta com praticamente a mesma velocidade. Comparado com a bola de boliche a bola de golfe logo após a colisão tem:
a) mais momento linear e menos energia cinética.
b) mais momento linear e mais energia cinética.
c) menos momento linear e menos energia cinética.
d) menos momento linear e mais energia cinética.
e) nenhuma das respostas anteriores.
Ver solução completaQuestão 113
Um trem é carregado com areia ao passar sob uma ponte. A areia é despejada nos vagões à taxa de 500kg por segundo. Como a areia é despejada verticalmente de uma altura de vários metros, ao atingir a caçamba do vagão, a velocidade dos grãos de areia é de cerca de 14m/s. A massa do vagão vazio é de 2.000kg, e é preenchido
com 6.000kg de areia ao passar sob a ponte.
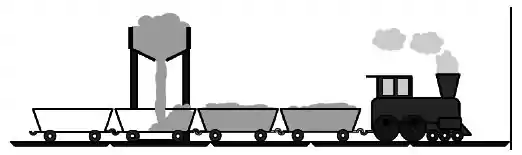
- Desprezando-se as perdas por atrito com os trilhos, determine a força que a locomotiva precisa fazer para puxar o trem a uma velocidade constante de 0,5m/s e a potência necessária para manter o movimento. Note que como o sistema não pode ser considerado como uma partícula não é conveniente a utilização do teorema trabalho-energia cinética.
- Determine a força suportada pelo trecho de trilhos sob um vagão quando este estiver 50% preenchido de areia. Suponha que o trecho de trilhos em questão suporta somente este vagão neste momento.
- Se a locomotiva desengatar do primeiro vagão quantos segundos se passarão até que o restante do trem reduza sua velocidade à metade da inicial? Suponha que a massa do restante do trem (incluindo a areia) seja de 10.000kg no instante do desengate.
Questão 114
Você está de pé em um skate, inicialmente em repouso. Um amigo joga uma bola muito pesada em sua direção. Você pode agarrar ou rebater a bola de volta para o seu amigo. Qual das opções minimizará a sua velocidade de recuo no skate?
a) agarrar a bola.
b) rebater a bola com uma velocidade maior do que a que foi originalmente lançada.
c) rebater a bola com a mesma velocidade que foi originalmente lançada.
d) sua velocidade de recuo no skate será a mesma, independentemente de você pegar a bola ou desviar a bola.
e) não é possível determinar se não conhecemos as massas do sistema.
Ver solução completaQuestão 115
5) Um canhão está preso em um carro que está sobre uma superfície plana e horizontal sem atrito. Inicialmente, o sistema se encontra em repouso e, em um determinado instante, o canhão dispara uma bala para a direita com velocidade horizontal de módulo , para um observador em repouso fora do carro. A bala é, então, capturada por uma armadilha que está firmemente presa ao carro. A figura ilustra tal situação.
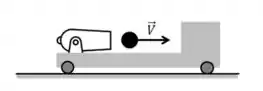
Sabendo que a bala de canhão tem massa menor que o resto do sistema, o que podemos concluir sobre a velocidade do sistema após a bala ter sido capturada?
(a) , para a esquerda.
(b) , para a direita.
(c)
(d) , para a direita.
(e) , para a direita.
Ver solução completaQuestão 116
Um carrinho de massa move-se em linha reta sobre um piso horizontal sem atrito com velocidade de . Sobre o carrinho encontra-se fixada na posição horizontal, uma mola que é comprimida por um bloco de massa . Inicialmente, o bloco se encontra preso ao carrinho por um fio comprimindo a mola. Em certo instante, o fio se rompe e a mola empurra o bloco para fora do carrinho, projetando-o com uma velocidade de em relação ao piso. Uma vez livre do bloco, qual a nova velocidade do carrinho?
a)
b)
c)
d)
e)
Ver solução completaQuestão 117
Um núcleo atômico , inicialmente em repouso, sofre uma desintegração radioativa, fragmentando-se em três partículas, cujos momentos lineares são , e . A figura mostra os vetores que representam os momentos lineares das partículas e , e , imediatamente após a desintegração. O vetor, que melhor representa o momento linear da partícula , , é:
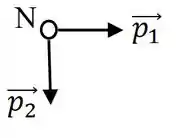
![]()
![]()


Questão 118
Uma bala de massa igual a 4, 5 g é disparada horizontalmente num bloco de madeira de massa igual a 2, 4 kg, em repouso sobre a superfície horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale 0,20. A bala fica retida no bloco que sofre um deslocamento de 1, 8 m até o repouso.
b. Qual a velocidade inicial da bala?
Ver solução completaQuestão 119
Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.
b. Quais as velocidades dos corpos após a colisão?
Ver solução completaQuestão 120
Um corpo de 4 kg, deslocando-se a 5 m/s, efetua uma colisão perfeitamente elástica com um corpo de 1 kg, inicialmente em repouso. Determine a velocidade final de cada corpo e a energia transferida para o corpo de 1 kg.
Ver solução completaQuestão 121
Um caminhão carregado, M = 3 ton, viajando para o norte a 60 km/h, colide com um carro de massa total m = 1 ton, trafegando para leste a 90 km/h, num cruzamento. Calcule em que direção e de que distância o carro é arrastado pelo caminhão, sabendo que o coeficiente de atrito cinético no local do acidente é 0,5.
Ver solução completaQuestão 122
Uma bola deslocando-se a 10 m/s, faz uma colisão perfeitamente elástica, mas oblíqua, com uma outra bola de mesma massa e em repouso. A bola incidente é desviada de 30◦ em relação à direção inicial do movimento. Determinar a velocidade de cada bola depois da colisão.
Ver solução completaQuestão 123
Num choque entre dois corpos de massas e , o primeiro desvia 90◦ de sua trajetória original, mantendo inalterada sua energia cinética. Se as velocidades iniciais dos corpos eram, respectivamente, e :
a. Calcule o vetor velocidade de após a colisão.
Ver solução completaQuestão 124
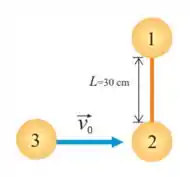
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.
(a) Determine o vetor posição do centro de massa em função do tempo.
Questão 125
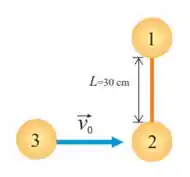
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.
(b) Determine o vetor velocidade do centro de massa.
Questão 126
Em uma colisão elástica bidimensional, vimos que o módulo do momento final do corpo incidente depende do ângulo de espalhamento da partícula, da razão entre as massas e do momento inicial da partícula incidente . No referencial em que a partícula 2 está inicialmente em repouso, esta relação é dada por
Quando as massas entre as partículas são próximas, qual o valor máximo do ângulo de espalhamento da partícula 1, , e o valor máximo do módulo do momento da partícula 2, nesta condição?
Questão 127
Uma esfera de massa é lançada em um trilho unidimensional de atrito desprezível com velocidade ao encontro de uma segunda esfera lançada simultaneamente de massa desconhecida com velocidade . As esferas colidem elasticamente e durante a colisão a primeira esfera sofre uma força dada pelo gráfico abaixo.
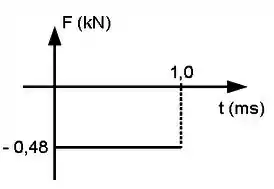
(b) Determine a velocidade imediatamente depois da colisão da primeira esfera.
(c) Determine a velocidade imediatamente depois da colisão da segunda esfera e o valor de sua massa.
Ver solução completaQuestão 128
Considere a colisão mostrada na figura. As massas dos blocos bem como as velocidades antes e depois da colisão são fornecidas.

A colisão é:
- Não é possível porque o momento linear não é conservado.
- É parcialmente não elástica.
- É perfeitamente elástica.
- É caracterizada por um aumento de energia cinética.
- É totalmente não elástica.
Questão 129
Uma bola de tênis, de massa e velocidade , é rebatida por um jogador, adquirindo uma velocidade de mesmo valor e direção que mas de sentido contrário. Qual foi a variação da quantidade de movimento da bola?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 130
Considere a seguinte colisão entre duas pequenas esferas de mesma massa. Antes do choque, elas possuem velocidades e , respectivamente, onde é uma constante positiva. Após a colisão, elas permanecem grudadas uma na outra com velocidade . Calcule o módulo de e o ângulo entre e o eixo .
Escolha uma:
Questão 131
Um caçador está parado sobre um lago congelado e essencialmente sem atrito, quando usa um rifle que dispara balas de a . A massa do caçador (incluindo sua arma) é , e o caçador segura a arma firmemente após o disparo. Ache a velocidade de recuo do caçador, caso ele dispare o rifle
(b) formando um ângulo de acima do plano horizontal.
Ver solução completaQuestão 132
Sobre uma mesa de ar horizontal sem atrito, o disco de hóquei A (com massa igual a ) se desloca ao encontro do disco B (com massa igual a ), que inicialmente está em repouso. Depois da colisão, o disco A possui velocidade igual a para a esquerda e o disco B possui velocidade igual a para a direita.
(a) Qual era a velocidade do disco A antes da colisão?
Ver solução completaQuestão 133
Um caçador está parado sobre um lago congelado e essencialmente sem atrito, quando usa um rifle que dispara balas de a . A massa do caçador (incluindo sua arma) é , e o caçador segura a arma firmemente após o disparo. Ache a velocidade de recuo do caçador, caso ele dispare o rifle
(a) horizontalmente.
Ver solução completaQuestão 134
Em um campo de futebol lamacento, um zagueiro de 110 kg se choca com um jogador meio de campo de 85 kg. Imediatamente antes da colisão, o zagueiro se deslocava com velocidade de 8,8 m/s para o norte e o outro jogador se deslocava com velocidade de 7,2 m/s para o leste. Qual é a velocidade (módulo, direção e sentido) com a qual os dois jogadores se movem unidos imediatamente após a colisão?
Ver solução completaQuestão 135
Uma bola de gude de 10,0 g desloca-se com velocidade de 0,400 m/s para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com outra bola de gude de 30,0 g que se desloca com velocidade de 0,200 m/s para a direita (Figura).
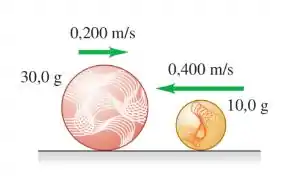
(b) Calcule a variação do momento linear (isto é, o momento linear depois da colisão menos o momento linear antes da colisão) para cada bola de gude. Compare os valores obtidos para cada bola.
Ver solução completaQuestão 136
Complete a seguinte afirmação: o momento linear (momentum) será conservado numa colisão de dois corpos se, e somente se,
- A colisão for elástica.
- A energia cinética do sistema se conservar.
- Ambos os corpos ficarem em repouso após a colisão.
- As forças internas do sistema de dois corpos se cancelarem em pares ação-reação.
- A força externa resultante sobre o sistema de dois corpos for zero.
Questão 137
Na comemoração com fogos de artifício do Réveillon, um rojão é lançado verticalmente e explode no ponto mais alto de sua trajetória em três partes, cada parte tendo uma massa de . Uma parte vai para a esquerda e outra vai diretamente para baixo, conforme é mostrado no diagrama. Qual é a direção mais provável da terceira parte?

a) Direção
b) Direção
c) Direção
d) Direção
e) Nenhuma dessas são prováveis de ocorrer.
Ver solução completaQuestão 138
Dois carrinhos de brinquedo de inércias e estão mantidos juntos um ao outro por uma mola comprimida entre eles. A energia inicialmente armazenada no sistema é . Quando o sistema é liberado, os carros estão livres para se mover.
- Se você medir a velocidade do carro de como para a direita, qual é a velocidade (módulo, direção e sentido) do outro carro?
- Considerando o sistema formado pelos dois carrinhos e pela mola, escreva a lei de energia para o sistema e determine a energia térmica perdida pelo sistema após a liberação dos carrinhos.
Questão 139
Considere um homem de , sentado em uma pista de gelo, lançando horizontalmente para frente uma bola de . A força de lançamento é dada pela função do tempo , válida no intervalo (este último é o instante em que a bola perde contato com a mão do homem). Desprezando todos os atritos e considerando que inicialmente homem e bola se encontram em repouso em relação à pista, determine:
(a) o módulo do impulso sobre a bola;
(b) o módulo da força média sobre a bola;
Se, após o lançamento, o homem recua no sentido positivo do eixo x, determine:
(c) os vetores e, respectivamente velocidade da bola e velocidade de recuo do homem.
Ver solução completaQuestão 140
Uma partícula de massa se move com velocidade e aproxima-se de outra partícula de mesma massa que está parada em uma superfície sem atrito. As duas partículas colidem obliquamente. Logo após a colisão a primeira partícula passa a se mover com uma velocidade de módulo fazendo um ângulo de acima da direção de seu movimento antes da colisão. A segunda partícula logo após a colisão passa se mover com uma velocidade com módulo fazendo um ângulo de abaixo da direção inicial que tinha a primeira partícula antes da colisão.
(b) Determine os módulos das velocidades das partículas e logo após a colisão.
(c) Determine se a colisão foi elástica ou inelástica.
Ver solução completaQuestão 141
Considere que as massas do projétil e do alvo são e , respectivamente. Se o módulo da velocidade inicial do projétil é , então o módulo da velocidade do alvo no instante em que ele perde contato com o projétil é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 142
Uma caixa explode em dois pedaços enquanto se movia com velocidade positiva ao longo de um eixo x (orientado para a direita). O pedaço da direita (de massa ) adquire uma velocidade positiva, mas o pedaço da esquerda (de massa ) pode ter velocidade positiva, negativa ou zero. Classifique os três resultados possíveis segundo o módulo de , do menor para o maior valor.

(A) a, b, c
(B) a, c, b
(C) b, a, c
(D) b, c, a
(E) c, a, b
Ver solução completaQuestão 143
Uma bala de massa m é disparada com uma velocidade horizontal igual a v0 atingindo um bloco de massa M = 4m onde acaba alojada. Após a colisão o bloco desliza sobre uma superfície plana. Entre os pontos A e B existe atrito entre o bloco e a superfície. A distância entre os pontos A e B é igual a d. O coeficiente de atrito cinético entre o bloco e a superfície é μ. Podemos considerar que colisão é praticamente instantânea e todas as distâncias são muito maiores do que o tamanho do bloco. A resistência do ar também pode ser desconsiderada. Expresse suas respostas em termos v0, m, d, μ e g.
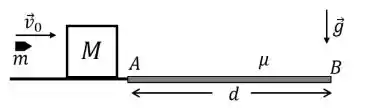
a) Determine a velocidade do conjunto bala+bloco imediatamente após a colisão. Justifique claramente as Leis de Conservação utilizadas.
b) Determine a velocidade do sistema após o conjunto percorrer à distância d. Justifique claramente as expressões utilizadas.
c) Determine o valor do módulo da velocidade inicial da bala, para que o conjunto bala+bloco atinja o repouso após percorrer à distância d.
Ver solução completaQuestão 144
Um pêndulo de comprimento e massa é solto do repouso a um ângulo de da vertical. Quando o pêndulo atinge a posição vertical, ele atinge uma caixa de massa , em repouso sobre uma mesa sem atrito. A mesa tem uma altura de , conforme figura. Usar, se necessário, as aproximações e .
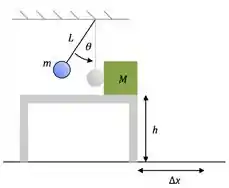
- Calcule a velocidade do pêndulo na posição vertical antes de atingir a caixa.
- Calcule a velocidade do pêndulo e da caixa logo após a colisão perfeitamente elástica.
- Determine o impulso sofrido pela caixa durante a colisão.
- Um carro de altura desprezível e massa é colocado na posição onde a caixa deveria cair no solo. A caixa cai sobre o carro e eles se grudam em uma colisão perfeitamente inelástica. Calcule a velocidade horizontal do carro logo após a caixa cair sobre ele.
Questão 145
Considere dois blocos de mesma massa que podem deslizar sobre uma superfície horizontal, sem atrito. Um deles está preso a uma mola ideal de constante elástica , inicialmente relaxada, como mostrado na figura. Num referencial inercial, a velocidade inicial do bloco solto tem módulo e aponta para a esquerda, e o bloco preso à mola está em repouso. Qual o valor da compressão máxima da mola?
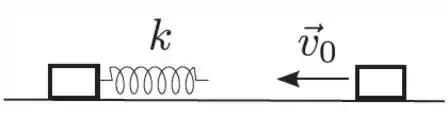
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 146
Um bloco em repouso postado sobre um plano horizontal sem atrito explode em fragmentos. O primeiro se desloca para a esquerda e tem massa e o segundo move-se para a direita.
O fragmento da esquerda atinge uma região de coeficiente de atrito cinético e percorre uma distância até parar.
O fragmento da direita entra em uma região de atrito cinético e percorre uma distância até chegar ao repouso.
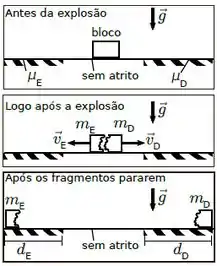
O módulo da aceleração gravitacional no local é . Determine:
- Os módulos das velocidades dos fragmentos da esquerda e da direita antes de entrarem nas regiões onde existe atrito.
- A massa do fragmento da direita.
- A variação da energia cinética do sistema entre os instantes antes e logo após a explosão.
Questão 147
Uma bola de tênis tem o módulo da velocidade de para baixo imediatamente antes de bater no chão. Ao atingir o solo a bola quica e abandona o chão com velocidade escalar de para cima. Qual das afirmações abaixo a respeito desta situação é verdadeira?
- O chão não produz nenhum impulso sobre a bola durante a colisão.
- A energia cinética da bola foi alterada pela colisão.
- A energia potencial gravitacional da bola foi alterada pela colisão.
- O momento linear da bola foi alterado pela colisão.
Questão 150
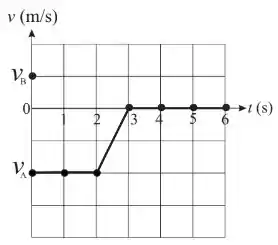
Duas partículas e , de massas e , interagem apenas entre si no intervalo . Elas deslocam-se em cima de uma mesa horizontal sem atrito ao longo do eixo . No instante , a partícula tem velocidade inicial enquanto a partícula tem velocidade inicial . Durante o intervalo de tempo observa-se, a cada segundo, a velocidade da partícula . O gráfico mostra a função obtida unindo-se por segmentos de reta os pontos experimentais representados por pequenos círculos.
Q5. Com base nos dados, determine a força média exercida pela partícula na partícula durante o tempo de colisão.
a)
b)
c)
d)
e)
Ver solução completaQuestão 151
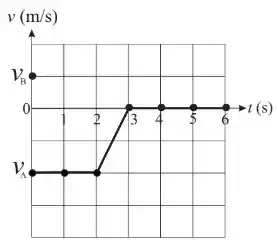
Duas partículas e , de massas e , interagem apenas entre si no intervalo . Elas deslocam-se em cima de uma mesa horizontal sem atrito ao longo do eixo . No instante , a partícula tem velocidade inicial enquanto a partícula tem velocidade inicial . Durante o intervalo de tempo observa-se, a cada segundo, a velocidade da partícula . O gráfico mostra a função obtida unindo-se por segmentos de reta os pontos experimentais representados por pequenos círculos.
Q6. Com base nos dados, determine a energia cinética do sistema formado pelas duas partículas quando e qual foi o tipo de colisão.
a)
b)
c)
d)
e)
Ver solução completa