Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.2 - Ex. 8
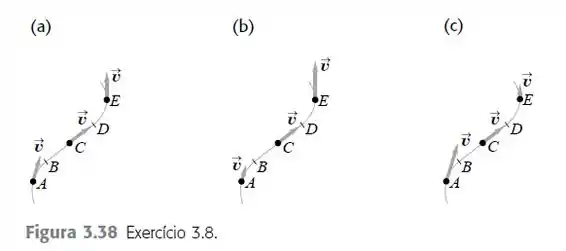
Uma partícula segue uma trajetória indicada na Figura 3.38. Entre os pontos B e D, a trajetória é uma linha reta. Desenhe o vetor aceleração em A, C e E para os casos em que a) a partícula
se move com velocidade escalar constante; b) a partícula se move com velocidade escalar que cresce uniformemente; c) a partícula se move com velocidade escalar que decresce uniformemente.
Passo 1
O componente da é perpendicular ao caminho está relacionado à mudança na direção de e a componente de é paralelo ao caminho está relacionado à mudança na magnitude de .
Quando a velocidade está aumentando, está na direção de e quando a velocidade está diminuindo, é oposto na direção de . Quando é constante, é zero e quando o caminho é uma linha reta, é zero.
Passo 2
Vamos esboçar os vetores de aceleração em cada caso:
é em direção ao centro da curvatura do caminho.
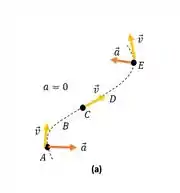
- Neste caso, a partícula está se movendo a uma velocidade constante. Isso significa que sua aceleração em linhas retas é zero. E sua aceleração em curvatura é a aceleração radial, o que significa que sua aceleração está direcionada para o centro dessa curvatura. Nas figuras fornecidas, vemos que a partícula está passando por duas curvaturas e uma linha reta enquanto se move a uma velocidade constante neste caso. Portanto, não há aceleração tangencial aqui, apenas a aceleração radial.
- Neste caso, a partícula está se movendo com aceleração constante enquanto acelera. Isso significa que sua aceleração, em linhas retas, é paralela e na mesma direção de sua velocidade. E sua aceleração em curvatura não é apenas radial; ela também possui um componente tangencial. Nas figuras fornecidas, vemos que a partícula está passando por duas curvaturas e uma linha reta enquanto acelera neste caso. Portanto, há um componente de aceleração tangencial, além da aceleração radial, no momento em que ela passa pela curvatura.
- Neste caso, a partícula está se movendo com aceleração constante enquanto desacelera. Isso significa que sua aceleração, em linhas retas, é paralela e na direção oposta à sua velocidade. E sua aceleração em curvatura não é apenas radial; ela também possui um componente tangencial. Nas figuras fornecidas, vemos que a partícula está passando por duas curvaturas e uma linha reta enquanto desacelera neste caso. Portanto, há um componente de aceleração tangencial, além da aceleração radial, no momento em que ela passa pela curvatura.
A aceleração no ponto A é a aceleração radial e está direcionada para a direita.
A aceleração em C é zero.
A aceleração em E é radial e está direcionada para a esquerda.
Agora é fácil esboçar as acelerações no caminho da partícula, como você vê abaixo.
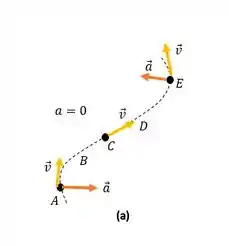
A aceleração no ponto A possui componentes radiais e tangenciais positivos. Assim, sua direção de aceleração está entre Leste e Norte.
A aceleração em C é paralela à linha reta (e na mesma direção de sua velocidade).
A aceleração em E possui componentes radiais e tangenciais positivos. Assim, sua direção de aceleração está entre Oeste e Norte. Agora é fácil esboçar as acelerações no caminho da partícula, como você vê abaixo.
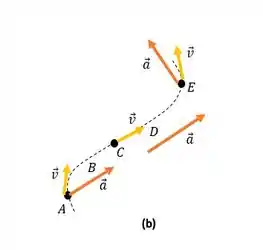
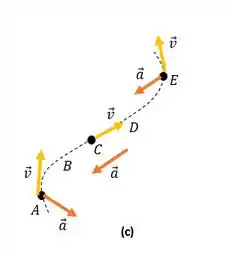
A aceleração no ponto A possui componentes radiais e tangenciais negativos. Assim, sua direção de aceleração está entre Leste e Sul.
A aceleração em C é paralela à linha reta (e na direção oposta à sua velocidade).
A aceleração em E possui componentes radiais e tangenciais negativos. Assim, sua direção de aceleração está entre Oeste e Sul. Agora é fácil esboçar as acelerações no caminho da partícula, como você vê abaixo.
Resposta
