Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 83
Um bloco de madeira de 2,0 kg está suspenso preso à extremidade inferior de uma haste de 1,0 kg e 1,0 m de comprimento. O bloco e a haste constituem um pêndulo que oscila sobre um eixo fixo livre de atrito que passa pela outra extremidade da haste. Uma bala de 10 g é disparada contra o bloco, onde se incrusta, fazendo o pêndulo oscilar até um ângulo de 30°. Qual era o valor de velocidade da bala? Você pode considerar o bloco de madeira como uma partícula.
Passo 1
Para o sistema (bala + bloco + haste), o momento angular é conservado. Depois que a bala fica presa no bloco, a energia mecânica do sistema é conservada. Suponha que o bloco seja pequeno.
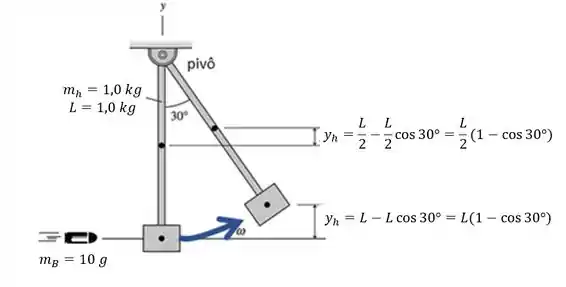
A origem do sistema de coordenadas foi colocada no centro de massa do bloco, que pendura livremente do fundo da haste.
Passo 2
O momento angular inicial do sistema em torno do pivô é devido apenas ao item:
O momento angular imediatamente após a bala atingir e furar o bloco é igual a . O momento de a inércia é
Isso implica que
Passo 3
O momento angular é conservado na colisão:
Precisamos determinar antes de encontrarmos . Para encontrar , usamos a equação de conservação da energia mecânica como o pêndulo oscila, o que é
Passo 4
A equação da energia pode ser ainda mais simplificada para
Finalmente, podemos usar a equação de conservação do momento angular para obter a velocidade da bala:
Uma velocidade de para uma bala é razoável.