Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.10 - Ex. 64b
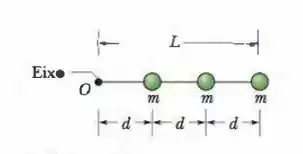
Na Figura abaixo, três partículas de 0,0100 kg foram coladas em uma barra, de comprimento L = 6,00 cm e massa desprezível, que pode girar em torno de um eixo perpendicular que passa pelo ponto O em uma das extremidades. Determine o trabalho necessário para mudar a velocidade angular (a) de O para 20,0 rad/s, (b) de 20,0 rad/s para 40,0 rad/s e (c) de 40,0 rad/s para 60,0 rad/s. (d) Qual é a inclinação da curva da energia cinética do conjunto (emjoules) em função do quadrado da velocidade angular (em radianos quadrados por segundo ao quadrado)?
Passo 1
Show de bolinhas pessoal, lembrando que:
Vamos obter:
Em que e . Logo:
Passo 2
Já o trabalho necessário para mudar a velocidade angular de para é dado pela relação:
Em que e . Sendo assim, vamos obter que:
Resposta
Exercícios de Livros Relacionados
9.39 Uma roda de carroça é feita como indicado na Figura 9.30. O raio da roda é igual a 0,300 m e o aro possui massa igual a 1,40 kg. Cada um dos seus oito raios, distribuídos ao longo de diâmetros, p
9.37 Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades. A barra possui 2,0 m de comprimento e massa de 4,0 kg, enquanto as bolas possuem 0,500 kg cada uma e podem ser tratadas
Pequenos blocos, todos com a mesma massa m , estão presos às extremidades e ao centro de uma barra leve de comprimento igual a L . Calcule o momento de inércia do sistema em relação a um eixo perpendi
9.35 Calcule o momento de inércia em relação a cada um dos seguintes objetos uniformes em relação aos eixos indicados. Se necessário, use as fórmulas da Tabela 9.2. a) Uma barra delgada de 2,50 kg e 7
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de 0,200k g , estão dispostas nos vértices de um quadrado de lado igual a 0,400m e conectadas por hastes leves (Figura 9.29 ).