27. Bob, com uma massa de , consegue arremessar uma pedra de com velocidade de . A distância percorrida por sua mão enquanto ela acelera a pedra do repouso até sua liberação é de .

Que valor de força constante Bob deve exercer sobre a pedra para arremessá-la com este valor de velocidade?

Se Bob está em pé sobre uma superfície de gelo sem atrito, qual é o valor de sua velocidade de recuo após a liberação da pedra?

Então galera nesse problema teremos que usar nossos conhecimentos de cinemática e o que aprendemos até agora das leis de Newton. Primeiro vamos fazer um diagrama de corpo livre de Bob e da pedra para analisarmos essa situação melhor.

Mas antes de irmos para o diagrama temos que nos atentar no detalhe crucial para esse problema, que envolve a terceira lei, é que a força que bob faz na pedra para lançá-la é a mesma que a pedra faz na mão de Bob, assim temos o seguinte:

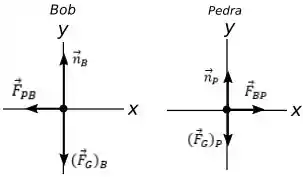
Vamos lá então, a força que é pedido em é nada mais é a que a força que o Bob aplica na pedra que é a mesma força que a pedra aplica em Bob , para achar essa força vamos usar a segunda lei de Newton, já que:

A massa da pedra já sabemos, falta encontrar a aceleração da pedra e podemos encontrá-la através da equação da velocidade da cinemática dada por:

A velocidade inicial da pedra é zero já que ela parte do repouso, a velocidade final é dada pelo enunciado e a distância percorrida enquanto Bob aplica a força na pedra.

Para encontrar a velocidade de recuo de Bob pedida em vamos usar outra equação da cinemática só que da seguinte forma:

Só que precisamos encontrar e , a aceleração podemos encontrar também através da segunda lei de Newton já que:

E sabemos a massa de Bob e a força que Bob sofre da pedra e podemos encontrar da mesma equação da cinemática acima só que para a pedra, assim:

Já que conhecemos tudo dos parâmetros da equação menos que é o temo em que Bob e a pedra estão em contato.