Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 39
39. A FIGURA P7.39 mostra um bloco de massa m em repouso sobre uma rampa com de inclinação. Os coeficientes de atrito do bloco com a superfície são e . Ele está ligado a outro bloco, de , suspenso por meio de uma corda sem massa que passa por uma polia também desprovida de massa e livre de atrito.
Qual é o mínimo valor de m para o qual o primeiro bloco ainda se mantém parado, sem deslizar?
Se esta massa mínima for cutucada ainda que ligeiramente, ela passará a subir a rampa. Que aceleração ela terá?
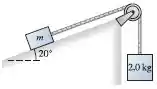
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada bloco do nosso sistema, temos o seguinte:
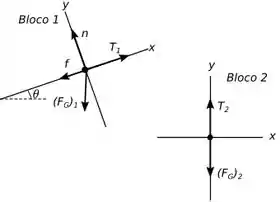
Vamos nos referir ao bloco da esquerda como bloco e o da direita como bloco .
Agora vamos analisar a nossa situação junto com o diagrama para ver se temos forças iguais presentes.
Como a corda não tem massa e não é deformada temos que .
Tanto para o item quanto para o item vamos analisar as forças de cada bloco usando a segunda lei de Newton e depois juntar as informações que obtemos.
Para o item teremos que os blocos estarão em repouso logo a força resultante é zero para os dois blocos e teremos um coeficiente de atrito estático para o bloco 1.
Para o item teremos os blocos em movimento e ambos com a mesma aceleração , já que eles estão presos e corda não deforma e teremos um coeficiente de atrito cinético para o bloco .
A massa do bloco para o item vai ser a mesma que encontramos em .
Passo 2
Vamos começar com o desenvolvimento para o item .
Vamos analisar o bloco na direção , temos:
Agora vamos analisar na direção para o mesmo bloco, temos:
Usando a expressão para força de atrito, temos:
Substituindo com a expressão que encontramos para normal , temos:
Passo 3
Agora vamos analisar o bloco , nesse bloco só tem motivo de analisar a direção , já que na não temos nenhum tipo de interação. Temos o seguinte:
Agora como dissemos no passo temos , assim temos que:
Isolando , temos o seguinte:
Substituindo os valores que conhecemos, temos:
Então temos que:
Passo 4
Agora vamos para o desenvolvimento do item , vamos começar analisando o bloco .
Agora nesse caso vamos só analisar na direção já que na direção vamos obter amesma coisa que encontramos no desenvolvimento de .
Temos o seguinte:
Agora usando o que já sabemos de , temos:
Agora vamos analisar o bloco na direção , temos o seguinte:
Usando o fato de que , temos:
Vamos isolar então. Temos:
Substituindo os valores que conhecemos, temos:
Então temos que: