Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 52
A cabeça de um martelo de , que se desloca de cima para baixo com velocidade de , pára, fazendo um prego penetrar em uma placa de pinho. Além de seu peso, existe uma força de aplicada de cima para baixo sobre o martelo por uma pessoa que o está usando. Suponha que a aceleração da cabeça do martelo seja constante durante o contato com o prego.
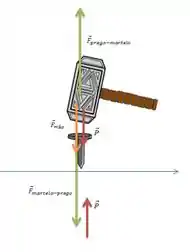
- Faça um diagrama do corpo livre para a cabeça do martelo . Identifique a força de reação a cada uma das forças incluídas no diagrama.
- Determine a força de cima para baixo exercida pela cabeça do martelo durante o contato com o prego.
- Suponha que o prego esteja em contato com madeira dura e que a cabeça do martelo só se desloque até parar. A força aplicada sobre o martelo é a mesma do item . Qual será então a força de cima para baixo durante o contato com o prego?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que a cabeça de um martelo de , que se desloca de cima para baixo com velocidade de , para, fazendo um prego penetrar em uma placa de pinho.
Além de seu peso, existe uma força de aplicada de cima para baixo sobre o martelo por uma pessoa que o está usando.
Suponha que a aceleração da cabeça do martelo seja constante durante o contato com o prego.
Queremos fazer o diagrama de corpo livre da cabeça do martelo. Para isso, precisaremos analisar todas as forças em todas as direções do corpo.
Com esse diagrama, poderemos determinar a força de cima para baixo exercida pela cabeça do martelo durante o contato com o prego.
Mas vamos interpretar melhor essa questão...
Passo 2
Sob a cabeça do martelo estão agindo três forças: a força peso orientada de cima para baixo de módulo , a força que a pessoa exerce sobre ele , também orientada de cima para baixo e de módulo e a força que o prego faz no martelo orientada de baixo para cima.
Essa última forma par ação reação com a força que o martelo faz no prego .
Tando a força resultante, quanto a aceleração do martelo vão apontar para cima, de modo que o diagrama de corpo livre fica assim ó:
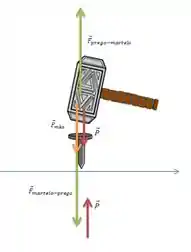
A força peso (em vermelho) é a força que a Terra faz no martelo e seu par ação reação é aplicada na Terra, feita pelo martelo.
A força que o martelo exerce no prego está representada em verde e a reação é a força que o prego exerce no martelo.
A força em laranja é a força extrena, feita pela mão da pessoa que está pregando esse prego.
Passo 3
Agora o problema pede para determinar a força , para isso precisamos primeiro determinar a aceleração. Os dados que o problema nos trás são:
Onde é a velocidade inicial, é a velocidade final e é a distância.
E usando a equação podemos determinar a aceleração:
Passo 4
A massa pode ser encontrada dividindo o peso pela gravidade :
E aplicando a segunda lei de Newton podemos determinar a força:
Essa é a força resultante! Mas o que queremos é a força exercida pela cabeça do martelo , que é a mesma que a força que o prego faz no martelo.
Pelo diagrama de forças temos:
Passo 5
Agora o deslocamento é menor, logo a aceleração vai ser outra consequentemente teremos outra força. Vamos fazer os mesmos passos para determinar a força .
Primeiro a aceleração!
Os dados que o problema nos trás são:
E usando a equação podemos determinar a aceleração:
E aplicando a segunda lei de Newton podemos determinar a força:
Essa é a força resultante! Mas o que queremos é a força exercida pela cabeça do martelo , que é a mesma que a força que o prego faz no martelo.
Passo 6
Pelo diagrama de forças temos:
Resposta
