Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 55

Um cabo de 20,0 m de comprimento consiste de um núcleo cilíndrico em níquel maciço, com 10,0 cm de diâmetro, envolto por uma casca cilíndrica em cobre, com 10,0 cm de diâmetro interno de 20,0 cm de diâmetro externo. A resistividade do níquel é igual a 7,8 × 10 - 3   Ω ⋅ m . (a) Qual é a resistência desse cabo? (b) Se considerarmos esse cabo como um material único, qual é a sua resistividade equivalente?

Passo 1

Os cabos C u e N i estão em paralelo. Para cada, R = ρ L / A .

O cabo composto é esboçado na Figura a seguir. A área da seção transversal do segmento de níquel é π a 2 e a área da porção de cobre é π ( b 2 - a 2 ) .

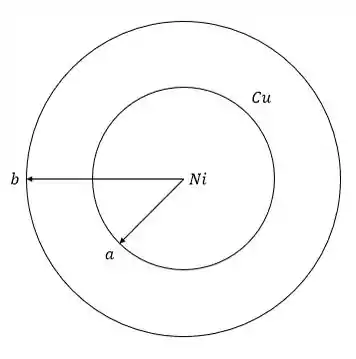
Para N i : ρ = 7,8 × 10 - 8 Ω ⋅ m

Para C u : ρ 1,72 × 10 - 8   Ω ⋅ m

Passo 2

  1. Assim, a resistência do cabo é dada por:

    2. 1 R c a b o = 1 R N i + 1 R C u .

    R N i = ρ N i L A = ρ N i L π a 2

    E

    R C u = ρ C u L A = ρ C u L π ( b 2 - a 2 ) .

    Portanto,

    1 R c a b o = π a 2 ρ N i L + π ( b 2 - a 2 ) ρ C u L .

    1 R c a b o = π L   a 2 ρ N i + b 2 - a 2 ρ C u = π 20   m   0,500   m 2 7,8 × 10 - 8   Ω ⋅ m + 0,100   m 2 - 0,050   m 2 1,72 × 10 - 8 Ω ⋅ m

    E

    R c a b o = 13,6 × 10 - 6   Ω = 13,6   μ   Ω

    Passo 3

  2. E a resistividade equivalente:

R = ρ L A = ρ L π b 2 .

Nos dá que

ρ = π b 2 R L = π 0,10 m 2 ( 13,6 × 10 - 6 Ω ) 20   m = 2,14 × 10 - 8 Ω ⋅ m  

resistividade efetiva do cabo é cerca de 25 % maior que a resistividade do cobre. Se o níquel tivesse resistência infinita e apenas a porção de cobre conduzida, a resistência do cabo seria de 14,6   μ Ω , o que não é muito maior que a resistência calculada na parte (a).

Resposta

  1. R c a b o = 13,6   μ   Ω
  2. 2,14 × 10 - 8 Ω ⋅ m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma combinação em série dos resistores A e B está conectada aos terminais de uma bateria. O resistor A tem o dobro da resistência do resistor B . Se a corrente conduzida pelo resistor A é I , então qu
Na Figura E26.11, a bateria possui fem igual a 35,0 V e resistência interna desprezível. R1 5,00 V. A corrente através de R1 é de 1,50 A, e a corrente através de R3 é de 4,50 A. Determine as correntes
Um resistor com R1 25,0 Ω está ligado a uma bateria com resistência interna desprezível e a energia elétrica é dissipada por R1 a uma taxa de 36,0 W. Se um segundo resistor com R2 15,0 Ω está ligado e
Um resistor de 42 V é ligado em paralelo a outro de 20 V e o conjunto é conectado a uma fonte de tensão cc de 240 V. (a) Qual é a resistência da ligação em paralelo? (b) Qual é a corrente total da com
No circuito indicado na Figura E26.18, E 36,0 V, R1 4,00 V, R2 6,00 V e R3 3,00 V. (a) Determine a diferença de potencial Vab entre os pontos a e b quando a chave S está aberta e quando está fechada.