|| O bloco B da repousa sobre uma superfície para a qual os valores dos coeficientes de atrito estático e cinético valem, respectivamente, e . As cordas são de massas desprezíveis. Qual é o máximo valor de massa do bloco A para o qual o sistema ainda se mantém em equilíbrio?
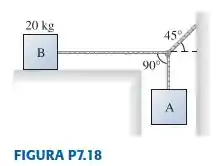
Passo 1
O sistema está em equilíbrio e as forças estão aplicadas de forma retangular, não precisaremos usar trigonometria explicita por que o componente horizontal da tensão é igual ao componente vertical da tensão. Assim, como o componente vertical da tensão é igual em módulo ao peso do bloco A. Então a tensão no cabo preso ao bloco B é igual ao peso do bloco A. Só que a tensão do bloco B é a força máxima possível de atrito estático.
Matematicamente:
Veja que não precisamos do coeficiente de atrito de do bloco A.