Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 57
Um estudante tenta erguer uma corrente que consiste de três elos idênticos. Cada elo possui massa de . Acorrente de três peças é conectada a um fio e depois suspensa verticalmente, com o estudante segurando a extremidade superior do fio e puxando de baixo para cima. Em função da força de puxar do estudante, uma força de baixo para cima de é aplicada sobre a corrente pelo fio.
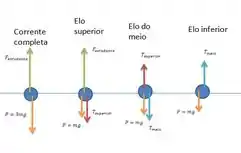
- Desenhe um diagrama do corpo livre para cada elo na corrente e também para a corrente toda considerada como um corpo único.
- Use os resultados do item (a) e as leis de Newton para determinar
- a aceleração da corrente e
- a força exercida pelo elo superior sobre o elo do meio.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um estudante tenta erguer uma corrente que consiste de três elos idênticos.
Cada elo possui massa de . Acorrente de três peças é conectada a um fio e depois suspensa verticalmente, com o estudante segurando a extremidade superior do fio e puxando de baixo para cima.
Em função da força de puxar do estudante, uma força de baixo para cima de é aplicada sobre a corrente pelo fio.
Queremos encontrar o diagrama de corpo livre para cada elo da corrente e para toda a corrente como se fosse um único corpo.
Para isso, precisaremos analisar todas as forças em todas as direções dos corpos.
Com isso, poderemos encontrar a aceleração da corrente e a força exercida pelo elo superior sobre o elo do meio.
Para isso, precisaremos aplicar a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Belezera pessoal, no sistema agem basicamente três forças: a força peso, a força que a estudante faz e a força de tensão que depende da posição relativa da corrente.
- Vamos analisar cada diagrama isoladamente:
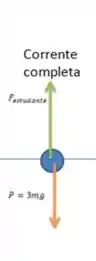
- Na corrente completa temos a força que o estudante puxa todo sistema, ela é responsável pela aceleração para cima.
-
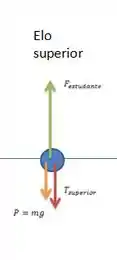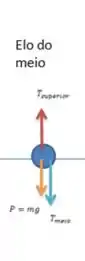
Considerando apenas o elo superior para soma, temos a força que o estudante exerce sobre o sistema, mas que é aplicada no elo de cima. - No elo central temos novamente três forças: a força que é a força que o elo de cima age no elo do meio, o peso referente apenas a massa desse elo e temos agora, da mesma maneira que no elo superior, temos uma força de tensão para baixo que é a força com que o elo inferior puxa o elo do meio, chamada de ;
- Por fim temos o elo inferior, nele agem duas forças: a força peso, também sobre apenas esse elo, e a força , mas essa agora apontando para cima.
Essa força aponta para cima e é vertical. Para baixo temos o peso referente a todos os elos, pois aqui consideramos a corrente como sendo inteiro, um corpo só;
Passo 3
Para baixo temos o peso, mas agora ao invés de considerar todas três partes da corrente, só consideramos um elo, por isso o peso é referente apenas uma massa . Também temos a força que os outros elos agem sobre esse elo de cima, chamada de ;
Passo 4
Passo 5
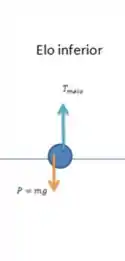
Passo 3
Aplicando a segunda lei no diagrama bem a esquerda teremos:
Logo:
Passo 4
Agora o problema quer saber a tensão exercida pelo elo superior, que chamamos de . Isolando o primeiro elo temos:
Como acabamos de determinar a aceleração, ficou tranquilo de encontrar a tensão no elo do meio:
Portanto:
Resposta
