Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.6 - Ex. 31
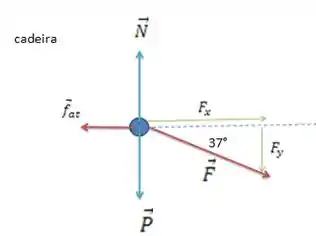
Uma cadeira com massa de está sobre um piso horizontal, que não está livre de atrito. Você empurra a cadeira com uma força , que forma um ângulo de abaixo da horizontal, e a cadeira desliza ao longo do piso.
- Faça um diagrama do corpo livre para a cadeira;
- Use seu diagrama e as leis de Newton para calcular a força normal que o piso exerce sobre a cadeira.
Passo 1
Eaeee, belezinha?? Bom... o enunciado nos diz que uma cadeira de está sobre um piso horizontal que não está livre de atrito (opa!! Então vamos usar força de atrito aqui ein).
Ainda, o enunciado diz que alguém empurra a cadeira com uma força , que forma um ângulo de abaixo da horizontal, e a cadeira desliza ao longo do piso.
Queremos fazer um diagrama de corpo livre da cadeira.
Para isso, temos que analisar todas as forças que estão atuando sobre a cadeira e em todas as direções.
Com isso, devemos calcular a força normal que o piso exerce sobre a cadeira.
Bora lá!! 😉
Passo 2
a) Primeiramente queremos o diagrama de corpo livre da cadeira. Esse diagrama mostra as forças externas atuando na cadeira.
Vamos começar identificando as forças atuando na cadeira:
- se a massa está sob um piso horizontal, então ela está em contato com uma superfíciel, logo existe uma força de reação ao contato: a força normal . Ela é perpendicular à superfície;
- se ela está próximo à superfície da Terra, como é o caso, esse objeto sobre a ação da gravidade (onde é a força peso). Essa força é vertical para baixo;
- a cadeira está em uma superfície que não é livre de atrito, portanto temos que considerar o atrito entre a cadeira e o chão ; Como a gente está empurrando a cadeira para a direita, a força de atrito está oposta ao movimento, para a esquerda.
- e por último, temos a força com que a cadeira é empurrada, a força , ela faz um ângulo de com a horizontal, no sentido horário. Aí podemos decompor essa força em suas componentes vertical e horizontal para trabalhar com elas depois.
Passo 3
Agora que identificamos essas forças, podemos fazer o diagrama do corpo livre:
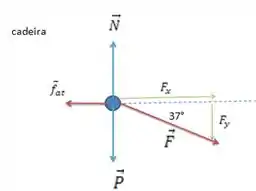
Passo 4
b) Sabemos que a cadeira desliza horizontalmente, mas permanece em repouso em relação à vertical. Sendo assim, as forças (ou suas componentes) na direção vertical estão todas equilibradas.
Na vertical temos o peso ( é a massa e é a aceleração da gravidade) para baixo, a componente vetical da força também para baixo e a força normal para cima e é exatamente essa última que queremos!
A gente achou essa componente vertical multiplicando o módulo da força pelo seno de , porque esse ângulo está oposto ao eixo vertical.
Como a massa da cadeira foi dada e também a força aplicada , podemos usar a equação de equilíbrio na vertical para essas forças e descobrir o valor de :
Resposta
