Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.6 - Ex. 62
Use a Equação (9.20) para calcular o momento de inércia de uma barra delgada de massa e comprimento em relação a um eixo perpendicular à barra e passando pela sua extremidade.
Passo 1
Falaaa, aí!
A gente quer o momento de inércia de uma barra delgada de massa , ou seja, a gente considera que ela só tem comprimento. E esse momento é em relação a um eixo perpendicular a barra, mas posicionado em sua extremidade. Algo assim:
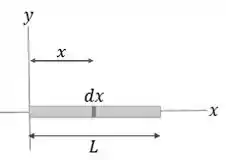
Sendo que queremos em relação a .
Ele manda a gente usar a expressão 9.20 que é:
O que a gente vai fazer é montar essa integral!
Passo 2
Primeiro, vamos achar quem é .
Vamos pegar o eixo ao longo da haste, com a origem na extremidade esquerda onde temos . E considerar uma fatia fina na coordenada e largura .
é a distância entre nosso eixo e nossa fatia, então
Só falta achar .
Bora lá!
Passo 3
é massa dessa fatia.
Podemos achar a densidade linear () dessa barra dividindo a massa total pelo comprimento da barra. Fica
Como a fatia tem comprimento , se a gente multiplicar esse comprimento pela densidade linear da barra, achamos a massa da fatia:
Tranquilo até aqui?
Passo 4
Então a integral fica
Mas como no nosso sistema de coordenadas nossa barra começa em e termina em , ficamos
Calculando, vamos tirar o que é constante da integral
Usando a regrinha de integrar polinômios:
E fim! Entendeu tudo? Responde Aí!
