Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 57
Uma caixa de está sobre uma rampa sem atrito inclinada de . Alguém puxa a caixa rampa acima com uma corda (Figura 4-44). Se a corda forma um ângulo de com a horizontal, qual é a menor força capaz de deslocar a caixa rampa acima?
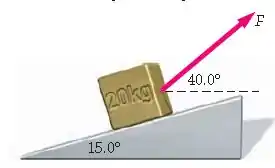
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre, mostra as forças que estão agindo na caixa quando o homem a puxa sobre a superfície sem atrito. Podemos aplicar a segunda lei de Newton para encontrar a força mínima necessária para mover a caixa.
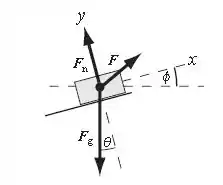
Sabemos que:
Substituindo os valores, temos:
Resposta
Exercícios de Livros Relacionados
E x . 5.8 mostra o gráfico da aceleração versus força para três objetos puxados por ligas de borracha. A massa do objeto 2 é 0,2 k g . Quais são as massas dos objetos 1 e 3 ? Explique seu raciocínio.
Um caixote contendo pratos delicados encontra-se na carroceria de um pequeno caminhão. Partindo de um semáforo, o veículo acelera para o norte, e o caixote se move sem escorregar. A força de atrito pa
Pode a força de atrito sobre um objeto apontar no mesmo sentido do movimento do objeto? Em casa afirmativo, dê um exemplo. Em caso negativo, explique.
Um astronauta em órbita da Terra segura nas mãos duas bolas com aparências externas idênticas. Entretanto, uma delas é oca, enquanto a outra é recheada com chumbo. Como pode o astronauta determinar qu
Com um passageiro dentro, um caixote é lançado diretamente para cima por um elástico gigantesco. Antes do arremesso, o passageiro ficou em pé sobre uma balança e mediu seu peso como 750 N. Após ter pe