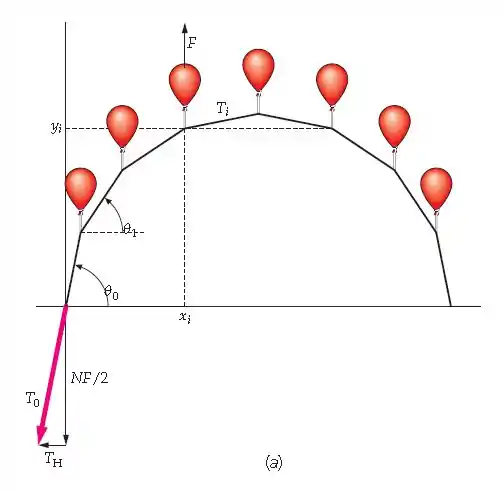
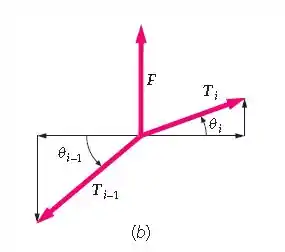
Arcos de balão são uma decoração encontrada em feiras e comemorações. Prende-se balões cheios de hélio a uma corda fixa ao chão pelas extremidades. A ascensão dos balões levanta a estrutura em uma forma de arco. A Figura 4-43a mostra a geometria de tal estrutura. N balões são amarrados em pontos igualmente espaçados ao longo de uma corda sem massa de comprimento L, que está presa a dois suportes nas extremidades. Cada balão contribui com uma força de sustentação de magnitude F. As coordenadas horizontal e vertical do ponto da corda onde está amarrado o i-ésimo balão são e e é a tensão no i-ésimo segmento. (Note que o segmento 0 é o segmento entre o ponto de amarração e o primeiro balão, e que o segmento N é o segmento entre o último balão e o outro ponto de amarração.) (a) A Figura 4-43b mostra um diagrama de corpo livre para o i-ésimo balão. Usando este diagrama, mostre que a componente horizontal da força , (chame-a de ) é a mesma para todos os segmentos da corda. (b) Considerando as componentes verticais das forças, use as leis de Newton para deuzir a seguinte relação entre as tensões nos i-ésimo e (i – 1)-ésimo segmentos : (c) Mostre que (d) Usando diagrama e as duas expressões anteriores, mostre que e que , .

Passo 1

Passo 2

Passo 3

Passo 4

Resposta