Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 62
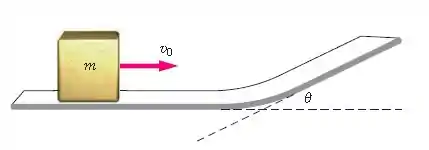
Um bloco de massa m escorrega sobre um piso sem atrito e depois sobre uma rampa sem atrito(Figura 4-48). O ângulo da rampa é e a rapidez do bloco antes de começar a subir a rampa é . O bloco escorregará até uma altura máxima h acima do piso, antes de parar. Mostre que h é independente de m e , deduzindo uma expressão para h em termos de
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. Ele quer que a gente ache que é altura máxima que esse bloco atinge quando chega na rampa, em função da sua velocidade inicial ao chegar na rampa e , a aceleração da gravidade.
O primeiro a se fazer, é desenhar o diagrama de corpo livre para entender melhor a situação do bloco quando ele passa pela rampa:
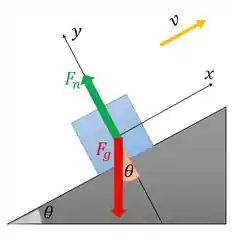
Como o bloco tem massa , ele vai estar sob ação da gravidade, ou seja, há a força peso puxando o bloco para baixo.
E como há contato entre o bloco e a superfície, a gente precisa considerar a força normal que a superfície aplica perpendicularmente ao bloco. Ele fala para desconsiderarmos o atrito, então com esse diagrama a gente já representou todas as nossas forças.
Escolhemos colocar um dos eixos coincidindo com o movimento do bloco, tá?
Então, a partir desse diagrama, a gente vai tentar achar . Vamos ver como fazer isso!
Passo 2
Temos , a velocidade do bloco antes de entrar na rampa. E temos que quando ele está na altura máxima, sua velocidade é nula .
E se a gente for fazer um esqueminha do movimento, teríamos algo assim:
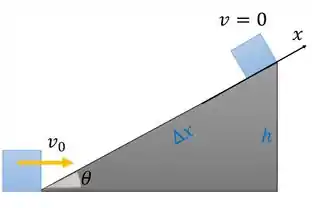
Podemos relacionar trigonometricamente o deslocamento com a altura atingida. Temos que:
Temos que o bloco vai desacelerar ao passar pela rampa por causa das forças constantes atuando. Então há uma aceleração constante na direção do movimento. Assim a gente pode usar a equação que relaciona deslocamento com velocidade inicial e final para esse tipo de caso:
Como a velocidade no ponto mais alto é nula, temos que:
Substituindo nossa expressão para e isolando quem a gente quer, o :
Passo 3
Mas percebe que é simplemente , que é a velocidade inicial do bloco:
A gente só não sabe quem é , a aceleração na direção .
Vamos aplicar a segunda lei de Newton nessa direção para encontrar a aceleração.
Sabemos que:
A única componente de força que a gente tem em que é não nula é , já que está na direção de . Sendo que porque aponta para o sentido negativo de e seu ângulo é oposto a . Substituindo essa força no somatório de componentes em
Isolando quem a gente quer:
Passo 4
Agora a gente tem uma expressão para aceleração. Vamos substituir essa bonita na expressão de :
Simplificando:
Prontinho! Provamos que não depende de e nem de como ele pediu. Só de e .