Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 21
21. Uma caixa de desliza para baixo sobre um longo plano inclinado de, sem atrito. Ela começa partindo do repouso no tempo no topo do plano , a uma altura de acima do solo.
a) Qual é a energia potencial da caixa em relação ao solo em?
b) Use as leis de Newton para encontrar a distância que a caixa percorre no intervalo e sua velocidade em.
c) Encontre a energia potencial e a energia cinética da caixa em t = 1,0 s.
d) Encontre a energia cinética e a velocidade da caixa assim que atinge o solo na base do plano inclinado.
Passo 1
a) Primeiramente é necessário traçar um esboço da situação exposta no problema, demonstrando as forças que agem na caixa durante sua queda, bem como apresentando um sistema de referencial para o seguinte modelo físico, conforme demonstrado abaixo:
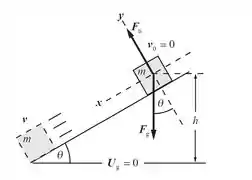
Baseado nessa imagem, podemos observar basicamente que duas forças agem na caixa durante sua queda: a força de contato entre a caixa e o plano inclinado e a força peso da caixa, a qual é responsável por impulsionar sua descida.
No instante inicial, vemos que a caixa tem velocidade nula e que ela encontra-se na altura máxima do plano inclinado. Logo o único tipo de energia presente nesse instante é a energia potencial gravitacional , a qual pode ser expressa em relação ao chão, no topo da inclinação por:
Substitui-se os então, os valores presentes no problema:
Passo 2
b) Para resolver esta etapa do problemas, é preciso atentar-se a diagrama de forças presenta na figura acima. Nele vemos que a componente da força peso da caixa no eixo contribui para provocar a aceleração nesse sentido. Desse modo, é conveniente começar a resolver o problema usando a equação do movimento uniforme acelerado como passo inicial.
Porém, a posição inicial ) é igual a 0 e a velocidade inicial é igual a zero, uma vez que a caixa parte do repouso . Desse modo:
Em seguida, aplicando o quando ela está descendo, encontra-se a aceleração desejada em
Mas, nada mais é do que a força gravitacional, igual a . Assim:
Finalmente, basta agora substituir a aceleração encontrada em na equação da posição em , para encontrar o quanto a caixa se deslocou de até.
Por último, para encontrar a velocidade em t = 1,0 s, basta utilizar a equação do movimento uniformemente acelerado para a velocidade Uma vez que é nula, temos que:
Passo 3
c) A energia cinética da caixano instante , uma vez já obtida sua velocidade nesse instante de tempo é dada por:
Para encontrar a energia potencial gravitacional no instante , considera-se o princípio da conservação de energia, o qual diz que a energia presente no começo do sistema é igual a energia presente no final. Logo, se no sistema há dois tipos de energia, respectivamente cinética e potencial gravitacional, basta subtrair a energia obtida no instante da energia cinética em a fim de encontrar a e energia potencial gravitacional no tempo desejado:
Passo 4
d) Parando bem pra analisar, assim que a caixa atinge o solo na base do plano inclinado, ela encontra-se na altura . Isso quer dizer que a caixa não tem energia potencial gravitacional em relação ao solo. Fica simples portanto, afirmar que no solo, pelo princípio da conservação da energia mecânica, a energia cinética final é igual a energia potencial no instante inicial . Logo . Para encontrar a velocidade nesse instante de tempo, basta igualar a já conhecida fórmula da energia cinética para chegar a resposta.
Resposta