Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 59

Uma caixa é mantida em posição, em um plano inclinado sem atrito, por um cabo (Figura 4-46). (a) Se θ = 60 ° e m = 50   k g , encontre a tensão no cabo e a força normal exercida pelo plano inclinado. (b) Encontre a tensão em função de θ e de m , e teste a plausibilidade de seu resultado para os casos especiais de θ = 0 ° e θ = 90 ° .

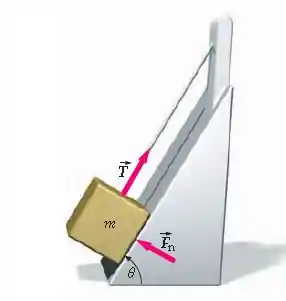
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O primeiro a se fazer, é desenhar o diagrama de corpo livre para entender melhor a situação.

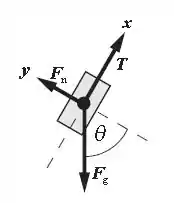
Vamos aplicar a segunda lei de Newton para encontrar a Tensão sobre o cabo. Observe que foi considerado um sistema de coordenadas e ele está exposto na figura.

Sabemos que:

∑ F x = m a x

No caso, o corpo está em equilíbrio, portanto sua aceleração é nula, logo:

∑ F x = T - F g sin ⁡ θ = 0

T = F g sin ⁡ θ = m g sin ⁡ θ

Substituindo os valores, temos:

T = 50 ⋅ 9,81 ⋅ sin ⁡ 60 °

T = 0,42   k N

Aplicando   ∑ F y = 0 , temos:

F n - F g cos ⁡ θ = 0

F n = F g cos ⁡ θ = m g cos ⁡ θ

Substituindo os valores, temos:

F n = 50 ⋅ 9,81 ⋅ cos ⁡ 60 °

F n = 0,25   k N

Passo 2

No passo 1, descobrimos que:

T = m g sin ⁡ θ

Aplicando θ = 90 ° , temos que:

T 90 = m g

Aplicando θ = 0 ° , temos que:

T 0 = 0

Os resultados são plausíveis.

Resposta

a ) T = 0,42   k N

F n = 0,25   k N

b ) T 90 = m g

T 0 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3. Um jogador de beisebol está deslizando em direção à segunda base. Identifique as forças exercidas sobre ele.
Experimente isso! Levante sua mão direita com a palma perpendicular ao chão, como se você estivesse pronto para bater palmas. Desse jeito, você não pode manter algo na palma da mão porque ele cairia d
No espaço, os astronautas "se pesam" oscilando sobre uma mola. Suponha que a posição de um astronauta de 75 kg que oscila dessa forma seja dada por x ( t )=0.30 ⋅ s e n ( π ⋅ t ) onde t está em segund
Considere - 0.80 n = 1500 a e n􏰐- ( 1.500⋅ 9,80 ) =0 �� Redija um problema realista para o qual essa equação se aplique..Desenhe um diagrama de corpo livre e uma representação pictórica para seu prob
Imagine-se suspenso por um enorme dinamômetro de mola enquanto o mesmo se move verticalmente com aceleração ay. Demonstre que a equação P=m g ( 1 + a g ) é a expressão correta para seu peso nesta situ