Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 5.Exercícios e Problemas - Ex. 3
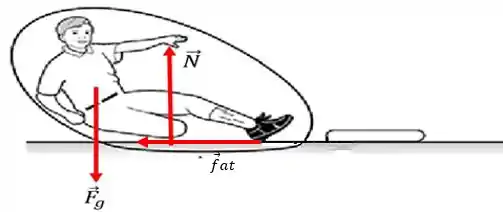
3. Um jogador de beisebol está deslizando em direção à segunda base. Identifique as forças exercidas sobre ele.
Passo 1
Opa! Aqui vamos nós de novo!
Olha só! De prache, já sabemos que existem duas forças exercidas sobre o jogador de beisebol... Que são:
Bom! A novidade aqui, em relação às questões anteriores; é que o atrito vai ocorrer nesse problema, devido ao fato de que o jogador está deslizando sobre a superfície. Se não tivesse atrito, o coitado ia ficar deslizando até chegar em Nárnia, rs rs rs.
Desse modo, obtemos a seguinte imagem abaixo...
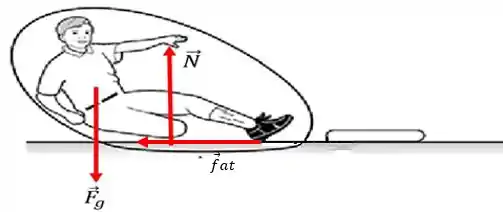
Onde é a nossa força de atrito.
E pronto! Terminamos aqui!
Resposta
Exercícios de Livros Relacionados
A família Zacchini ficou famosa pelos números de circo em que um membro da família era disparado de um canhão com a ajuda de elásticos ou ar comprimido. Em uma versão do número, Emanuel Zacchini foi d
Na Fig. 5-43, uma corrente composta por cinco elos, cada um de massa 0,100k g , é erguida verticalmente com uma aceleração constante de módulo a = 2,50m / s ² ². Determine o módulo (a) da força exerci
Um arremessador de peso lança um peso de 7 , 260k g empurrando-o ao longo de uma linha reta com 1 , 650m de comprimento e um ângulo de 34,10 ° com a horizontal, acelerando o peso até a velocidade de l
Um balde com água pesando 4,80 kg é acelerado de baixo para cima por uma corda de massa desprezível cuja tensão de ruptura é igual a 75 N. Calcule a aceleração máxima de baixo para cima que o balde po
Um objeto com massa m se move ao longo do eixo Ox. Sua posição em função do tempo é dada por x ( t ) =A t -B t 3 ,onde A e B são constantes. Calcule a força resultante sobre o objeto em função do temp