Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 91
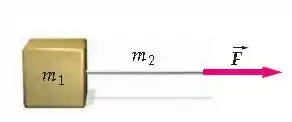
Uma caixa de massa é puxada sobre uma superfície horizontal sem atrito, por uma força que é aplicada à extremidade de uma corda de massa (veja a Figura 4-63). Suponha que a corda se mantém na horizontal. (a) Encontre a aceleração da corda e do bloco, olhando-os como um único objeto. (b) qual é a força resultante sobre a corda? (c) Encontre a tensão na corda no ponto onde ela está presa ao bloco.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando a segunda lei de Newton, temos:
Passo 2
Item (b):
Aplicando , para a corda, temos:
Do Passo 1, sabemos quem é , logo:
Passo 3
Item (c):
Aplicando , para o bloco, temos:
Do Passo 1, sabemos quem é , logo:
Resposta
Exercícios de Livros Relacionados
Você viaja em um elevador. Descreva duas situações nas quais seu peso aparente é maior que seu peso real.
Se você colocar suavemente um prato de louça fina sobre a mesa, ele não se quebrará. No entanto, se você o largar de uma altura, ele poderá muito bem se quebrar. Discuta as forças que atuam sobre o pr
Você puxa verticalmente, pelo fio de pesca, a partir do repouso, um peixe que acabou de pescar, para dentro de seu barco. Desenhe o diagrama de corpo livre do peixe após deixar a água e enquanto ganha
Para cada caso, identifique a força (incluindo a orientação) que causa a aceleração. (a) Um velocista ao ser dada a largada. (b) Um disco de hóquei deslizando livremente, mas sendo lentamente levado a
Um homem de 80 kg puxa seu filho de 40 kg com uma força de 100 N, os dois de patins sobre o gelo. Juntos , eles deslizam sobre o gelo ganhando rapidez a uma taxa constante. (a) A força exercida pelo m