Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 88

Um bloco de 50   k g ésta suspenso de uma corrente uniforme de 1,5   m   de comprimento que está pendurada do teto. A massa da corrente é 20   k g . Determine a tensão na corrente (a) no ponto onde a corrente está presa ao bloco, (b) no meio da corrente e (c) no ponto onde a corrente está presa ao teto.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O problema nos pede, em cada item, a tensão correspondente em cada ponto. Vamos analisar cada item. Para o item (a), queremos a tensão no ponto onde a corrente está presa ao teto.

O diagrama de corpo livre para esta situação está exposto abaixo:

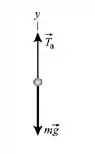
É possível observar que no ponto onde o bloco toca a corrente, somente o peso do bloco irá influenciar na tensão. Logo:

Aplicando ∑ F → = m a → , temos:

∑ F y = m a y

T a - m g = 0

T a = m g

Substituindo os valores, temos:

T a = ( 50   k g ) ( 9,81   m / s 2 )

T a = 490,5   N

Passo 2

Para o item (b), queremos a tensão no meio da corrente.

O diagrama de corpo livre para esta situação está exposto abaixo:

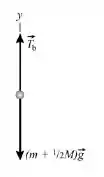
É possível observar que no meio da corrente, existe o peso de meia corrente e o peso do bloco que influenciam na tensão. Logo:

Aplicando ∑ F → = m a → , temos:

∑ F y = m a y

T b - m + 1 2 M g = 0

T b = m + 1 2 M g

Substituindo os valores, temos:

T b = ( 50   k g ) + 1 2 ( 2 0   k g ) ( 9,81   m / s 2 )

T b = ( 60   k g ) ( 9,81   m / s 2 )

T b = 588,6   N

Passo 3

Para o item (c), queremos a tensão no ponto onde a corrente está presa ao teto.

O diagrama de corpo livre para esta situação está exposto abaixo:

É possível observar que no ponto onde a corrente está presa ao teto, existe o peso da corrente e o peso do bloco que influenciam na tensão. Logo:

Aplicando ∑ F → = m a → , temos:

∑ F y = m a y

T c - m + M g = 0

T c = m + M g

Substituindo os valores, temos:

T c = ( 50   k g ) + ( 20   k g ) ( 9,81   m / s 2 )

T c = ( 7 0   k g ) ( 9,81   m / s 2 )

T c = 686,7   N

Resposta

a )   T a = 490,5   N

b )   T b = 588,6   N

c )   T c = 686,7   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em lugar de realizar a experiência da pg. 69 aplicando a força F através de um esforço muscular, podemos aplicá-la ao disco D de massa m através da força-peso de uma massa m’ suspensa da forma indicad
No sistema de figura, o bloco 1 tem massa de 10 Kg e seu coeficiente de atrito estático com o plano inclinado é de 0,5. Entre que valores mínimo e máximo pode variar a massa m do bloco 2 para que o si
No sistema da figura, m 1 = 20K g ,m 2 = 40K gem 3 = 60K g . Desprezando as massas das polias e dos fios e o atrito, calcule a aceleração do sistema e as tensões nos fios 1,2 e 3.
No sistema da figura ( máquina de Atwood) , mostre que a aceleração a da massa M e a tensão T da orda( desprezando as masss da corda e da polia) são dadas por a = M - m M + m g T = 2 m M M + m g
Um pintor está sobre uma plataforma suspensa de uma polia. Puxando a corda em 3, ele faz a plataforma subir com aceleração g/4. A massa do pintor é de 80 Kg e a da plataforma é de 40 Kg. Calcule as te