Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.1 - Ex. 11
Uma caixa de papelão de é puxada em uma esteira de bagagem sem atrito, inclinada em acima da horizontal por uma corda que exerce uma força de paralela à superfície da rampa. Se a caixa atravessa ao longo da superfície da rampa, calcule o trabalho realizado sobre ela (a) pela corda, (b) pela gravidade e (c) pela força normal da rampa. (d) Qual é o trabalho resultante realizado sobre a caixa? (e) Considere que a corda tenha um ângulo de acima da horizontal, em vez de ser paralela à superfície da rampa. Qual é o trabalho que a corda realiza sobre a caixa neste caso?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o trabalho realizado sobre a caixa pela corda, pela gravidade e pela força normal da rampa, além do trabalho resultante realizado sobre a caixa.
O primeiro passo é desenhar as forças que agem sobre o pacote ao descer o plano inclinado:
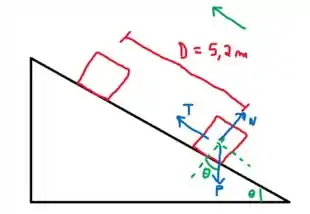
Observe que a força de tração está a favor do movimento, de modo que seu trabalho deve ser positivo, enquanto o da força peso deve ser negativo.
A definição do trabalho de uma força constante é
Então, vamos analisar cada força atuante no sistema, com suas componentes, e determinar o trabalho fazendo o produto da força pelo deslocamento.
Vamos lá!
Passo 2
Vamos calcular primeiro o trabalho da tração:
Onde é a tensão na corda e é o ângulo entre a corda e o deslocamento , que é nulo, por isso usamos o cosseno de :
Passo 3
Já para a força normal, como ela é perpendicular ao deslocamento, temos que
E para o peso, vemos que o ângulo que a força faz com o deslocamento é , logo:
Mas , de modo que
Passo 4
O trabalho da resultante é igual a soma dos trabalhos:
Portanto,
O trabalho positivo indica que a força resultante está acelerando o bloco!
Passo 5
No item (e) temos que considerar um ângulo de entre a corda e a horizontal, de modo que o ângulo entre a corda é o deslocamento é . Assim,
Fazendo as contas:
Observe que esse trabalho ainda supera o módulo do trabalho do peso (força resistente), de modo que o bloco ainda seria acelerado para cima ao longo do plano inclinado.
Valeu, galera! Até a próxima! 😉