Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.2 - Ex. 30
Um bloco de gelo com massa de desliza de cima para baixo ao longo de um plano inclinado de abaixo da horizontal. Sabendo que o bloco de gelo parte sem velocidade inicial, qual é sua velocidade final? Despreze o atrito.
Passo 1
Fala galerinha, beleza?
Todo o ponto desse problema é usar o teorema trabalho-energia para achar a velocidade do bloco depois dele descer no plano inclinado. Para isso, usamos que o trabalho da força resultante é igual a variação da energia cinética:
Como o bloco parte do repouso, temos que , de modo que
Passo 2
O maior desafio desse problema é calcular o trabalho da fora resultante sobre o bloco. Para isso, desenhamos as forças que agem sobre o bloco:
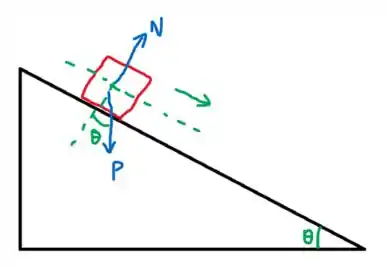
O trabalho da resultante será a soma dos trabalhos de cada força:
O trabalho da força normal é nulo, de modo que
Observe que o ângulo entre o peso e o deslocamento é . Assim,
Logo,
Com isso, podemos achar a velocidade