Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 42

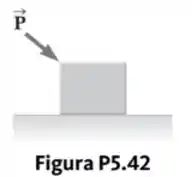
Uma caixa de peso F g é empurrada por uma força   P → sobre um chão horizontal, como mostrado na Figura P5.42. O coeficiente do atrito estático é μ s , e   P → é direcionada no ângulo θ abaixo da horizontal.

  1. Mostre que o valor mínimo de P que irá mover a caixa é dado por

    2. P = μ s F g sec ⁡ θ 1 - μ s t g   θ

  2. Encontre a condição em θ em termos de μ s para a qual o movimento da caixa é impossível para qualquer valor de P .

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo e bora!

Letra a:

A caixa está em equilíbrio, pouco antes de começar a se mover. Seja a força normal agindo sobre ele n e a força de atrito, f s :

No eixo vertical ∑ F y = m a y nos dá:

n = F g + Psin ⁡ θ

No eixo horizontal ∑ F x = m a x nos dá:

Pcos ⁡ θ = f

Mas como f s ≤ μ s n , então:

Pcos ⁡ θ ≤ μ s F g + Psin ⁡ θ

P cos ⁡ θ - μ s sin ⁡ θ ≤ μ s F g

P 1 - μ s tan ⁡ θ ≤ μ s F g sec ⁡ θ

P mínimo   = μ s F g sec ⁡ θ 1 - μ s tan ⁡ θ

Passo 2

Letra b:

Para colocar a caixa em movimento, a componente x   ( P c o s ⁡ θ ) deve superar o atrito f s = μ s n :

Pcos ⁡ θ ≥ μ s n = μ s F g + Psin ⁡ θ P cos ⁡ θ - μ s sin ⁡ θ ≥ μ s F g

Para que essa condição seja satisfeita, deve ser verdade que:

cos ⁡ θ - μ s sin ⁡ θ > 0 → μ s tan ⁡ θ < 1 → tan ⁡ θ < 1 μ s

Se esta condição não for atendida, nenhum valor de P pode mover a caixa.

Resposta

  1. P m ínimo   = μ s F g sec ⁡ θ 1 - μ s tan ⁡ θ
  2. tan ⁡ θ < 1 μ s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de aço de 11k g está em repouso sobre uma mesa horizontal. O coeficiente de atrito estático entre o bloco e a mesa é 0,52 . (a) Qual é o módulo da força horizontal que coloca o bloco na iminê
Quando uma pequena moeda de 2,0g é colocada a uma distância de 5,0c m do centro de um prato giratório horizontal que executa três rotações completas em 3,14s , a moeda não escorrega. Determine (a) a v
102- Uma força de 100 N, que faz um ângulo θ para cima com um piso horizontal, é aplicada a uma cadeira de 25,0 kg em repouso no piso. Se θ = 0°, determine (a) a componente horizontal F h da força apl
Uma caixa permanece parada depois de ter sido colocada em uma rampa inclinada a um ângulo com a horizontal. Qual(is) das seguintes afirmações é(são) correta(s) sobre o módulo da força de atrito que at
Para atender a uma exigência do serviço postal dos EUA, os calçados dos funcionários devem ter um coeficiente de atrito estático mínimo de 0,5 em uma superfície cerâmica. Um sapato atlético típico tem